写在前面

这一篇介绍了奇异谱分析与滤波器的关系，通过特征向量构造的特征滤波器可以用来描述奇异谱分析的二阶导滤波器^[1]。特殊结构的矩阵对应的滤波器具有更强的结论^[2]。此外本文还附带了降秩问题的滤波器视角^[3]，分别从截断奇异值分解和截断商奇异值分解两个方面介绍。

奇异谱分析

给定长度为\(N\)的信号\(\mathbf x=(x_0,\ldots,x_n,\ldots,x_N)\)，对于的轨迹矩阵记为\(\mathbf A\)。对\(\mathbf A\)进行奇异值分解 \[ \mathbf A=\mathbf U\mathbf \Sigma \mathbf V^T=\sum_{r=1}^{\text{rank}(A)}\sigma_r \mathbf u_r \mathbf v_r^T \] 根据特征值分解和奇异值分解的关系，有 \[ \begin{aligned} \mathbf A\mathbf A^T \mathbf u_r &= \sigma_r^2 \mathbf u_r\\ \mathbf A^T\mathbf A\mathbf v_r &= \sigma_r^2 \mathbf v_r\\ \mathbf U^T\mathbf A &= \mathbf U^T\mathbf U\mathbf \Sigma \mathbf V^T = \Sigma \mathbf V^T\\ \mathbf A^T \mathbf u_r &= \sigma_r\mathbf v_r \end{aligned} \] 记主成分\(\mathbf w_r=\sigma_r \mathbf v_r=\mathbf A^T \mathbf u_r\)，该向量的第\(k+1\)个元素表示为 \[ w_k^{(r)}=\sum_{l=0}^{L-1}u_l^{(r)}x_{l+k} \] 记第\(r\)个基本矩阵\(\mathbf A_r=\sigma_r \mathbf u_r \mathbf v_r^T=\mathbf u_r\mathbf w_r^T\)。由F范数和SVD的性质，显然有 \[ \|\mathbf A_r\|^2=\sigma_r^2,\|\mathbf A\|^2=\sum_{r=1}^{\text{rank}(A)}\sigma_r^2 \] 分组步骤则是将基本矩阵\(\{\mathbf A_r|r=1,\ldots,\text{rank}(A)\}\)分为若干个不先交的子集\(\{\mathbf A_r|r\in I_m\}\)，得到的分组矩阵为 \[ \mathbf A_{I_m}=\sum_{r\in I_m}\mathbf A_r \] 对角平均步骤则是从分组的基本矩阵\(\mathbf A_{I_m}\)中恢复出长度为\(N\)的时间序列 \[ \widetilde{\mathbf{x}}_{n}^{(r)}=\left\{\begin{array}{ll} \frac{1}{n+1} \sum_{i=0}^{n} u_{i}^{(r)} w_{n-i}^{(r)} & \text { for } 0 \leq n<L-1 \\ \frac{1}{L} \sum_{i=0}^{L-1} u_{i}^{(r)} w_{n-i}^{(r)} & \text { for } L-1 \leq n<K, \\ \frac{1}{N-n} \sum_{i=n-K+1}^{N-K} u_{i}^{(r)} w_{n-i}^{(r)} & \text { for } K \leq n<N \end{array}\right. \]

滤波器性质

向量\(\mathbf w_r\)是滑动平均滤波器对原始序列\(\mathbf x\)的滤波结果，其滤波器系数由特征向量\(\mathbf u_r\)倒序构成(reverse order)。因此类似特征向量得到的滤波器被称为特征滤波器(eigenfilter)，其传递函数如下 \[ F_r(z)=\sum_{l=0}^{L-1} u_{Z-l}^{(r)}z^{-l}=\sum_{l=0}^{L-1} u_{l}^{(r)}z^{Z-l} \] 对角平均步骤也可视为一个滑动平均滤波器，其系数为由特征向量\(\mathbf u_r\)正序构成(forward order)。其传递函数如下 \[ G_r(z)=\frac{1}{L}\sum_{l=0}^{L-1}u_l^{(r)}z^l \] SSA的其他步骤不涉及滤波器，因此也可将SSA视为一个二阶段滤波器。整个传递函数可由分解步骤的滤波器\(F_r(z)\)和对角平均步骤的滤波器\(G_r(z)\)的乘积组成 \[ H_r(z)=F_r(z)G_r(z)=\frac{1}{L}\sum_{l=-(L-1)}^{L-1}v_l^{(r)}z^l \] 由于滤波器\(F_r(z)\)和\(G_r(z)\)的系数元素相同，仅顺序不同，因此卷积和关于均值项是对称的(the convolution sum is symmetric about the mean term)，即 \[ v_l^{(r)}=v_{-l}^{(r)},l=1,\ldots,L-1 \] 实际上，这种对称性会导致实数值传递函数以及相关的频率响应 \[ H_r(z)=\sum_{l=-(L-1)}^{L-1}v_l^{(r)}e^{j2\pi lf}=v_0^{(r)}+\sum_{l=1}^{L-1}2v_l^{(r)}\cos(j2\pi lf) \] 滤波器\(H_r(z)\)会产生一个零相位的响应，即输入和输出之间没有时延。在区间\([L,K]\)以外部分，重构的结果可视为具有边界性质的二阶段滤波器。

周期图

周期图(periodogram)\(\mathcal P_x\)是时间序列对功率谱密度的估计，其定义为 \[ \mathcal P_x(k/N)=\left|\sum_{n=0}^{N-1}x_ne^{-j2\pi kn/N}\right|^2=\left|X_k\right|^2 \] 其中序列的离散傅里叶变换(DFT)\(X_k=\sum_{n=0}^{N-1}x_ne^{-j2\pi nk/N}\)。周期图的另一个替代定义 \[ \Pi_x(k/N)=\frac{1}{N} \begin{cases} 2\left|X_k\right|^2,&0<k<N/2\\ \left|X_k\right|^2,&k=0 \text{, or } N/2 \text{($N$ is even)} \end{cases} \] 显然有 \[ \sum_{n=1}^Nx_n^2=\sum_{k=0}^{\lfloor N/2\rfloor}\Pi_x(k/N) \]

特征滤波器的频率特性

周期图是基于DFT的频谱估计方法，特征滤波器的频率响应可通过周期图来估计。但是周期图频率集合是离散且\(L\)尺寸的，其中\(L\)是嵌入维度，也是特征滤波器的维数，这表明频率分辨率\(\delta_f = \frac{f_s}{L}\)。

当\(L\)取得比较小时，特征向量的频率特征可能会因频谱分辨率低而受到影响，因为无法区分非常接近的频率分量，并且能量会分散在属于离散集的最接近的频率之间：\(\{f_\Pi(k)=(0,\frac{1}{N},\frac{2}{N},\ldots,\frac{\lfloor N/2\rfloor}{N})f_s\}\)。

另一方面，滤波器的频率响应完全由特征向量组成的系数决定。 因此，\(H_r(f)\)提供了一种以连续方式确定特征滤波器频率响应的分析方法。

降秩问题与FIR滤波

去噪导向的降秩算法步骤如下：

• 根据输入信号形成Hankel（或Toeplitz）矩阵。

• 计算该矩阵的奇异值分解（SVD）

• 丢弃小的奇异值以获得秩降低的矩阵

• 通过沿其反对角线（或对角线）进行算术平均，从该通常非结构化的矩阵构造输出信号

该流程的核心是截断奇异值分解(TSVD)。信号的预白化涉及的变化是一个滤波器构造的降秩矩阵，可以通过截断的商奇异值分解(TQSVD)来获得。通过无穷序列信号和谱分析可以阐述降秩技术的谱性质。SVD可产生信号的能量分解，大的奇异值对应的重构信号分量是功率较高的分量。但是，到目前为止，对于应用于有限持续时间（短时间）信号的秩降低的频谱行为，尚未得出明确的结果。

符号说明

令\(n\times n\)矩阵\(J\)为换序矩阵，当右乘\(J\)时矩阵的列按照反序排列。显然\(JJ\)为单位阵。记\(\mathcal H(\boldsymbol x)\)和\(\mathcal H_p(\boldsymbol x)\)为如下的两种Hankel化算子 \[ \begin{aligned} \mathcal H(\boldsymbol x)=\begin{pmatrix} x_1&x_2&\ldots&x_n\\ x_2&x_3&\ldots&x_{n+1}\\ \vdots&\vdots&&\vdots\\ x_m&x_{m+1}&\ldots&x_{N} \end{pmatrix}\\ \mathcal H_p(\boldsymbol x)=\begin{pmatrix} 0&0&\ldots&x_1\\ \vdots&\vdots&&\vdots\\ 0&x_1&\ldots&x_{n-1}\\ x_1&x_2&\ldots&x_n\\ x_2&x_3&\ldots&x_{n+1}\\ \vdots&\vdots&&\vdots\\ x_m&x_{m+1}&\ldots&x_{N}\\ x_{m+1}&x_{m+2}&\ldots&0\\ \vdots&\vdots&&\vdots\\ x_N&0&\ldots&0 \end{pmatrix} \end{aligned} \]

• 可以通过改变Hankel矩阵的列来构造Toeplitz矩阵，即

\[ \mathcal T(\boldsymbol x)=\mathcal H(\boldsymbol x)J,\mathcal T_p(\boldsymbol x)=\mathcal H_p(\boldsymbol x)J \]

• 矩阵\(\mathcal H(\boldsymbol x)\)和\(\mathcal H_p(\boldsymbol x)\)右乘向量\(\boldsymbol y\)可视为对信号\(\boldsymbol x\)进行滤波，FIR滤波器系数为向量\(\boldsymbol y\)的分量。

• 区别在于\(\mathcal H(\boldsymbol x)\boldsymbol y\)的结果为长度\(m<N\)的向量，不包含端点效应；而\(\mathcal H_p(\boldsymbol x)\boldsymbol y\)的结果为长度\(N+n-1\)的向量，包含端点效应。

• 类似的，矩阵\(\mathcal T(\boldsymbol x)\)和\(\mathcal T_p(\boldsymbol x)\)右乘向量\(\boldsymbol y\)可视为对信号\(\boldsymbol x\)进行滤波

\[ \mathcal T(\boldsymbol x)\boldsymbol y=\mathcal H(\boldsymbol x)(J\boldsymbol y),\mathcal T_p(\boldsymbol x)\boldsymbol y=\mathcal H_p(\boldsymbol x)(J\boldsymbol y), \]

对角平均算子\(\mathcal A\)作用在矩阵\(M\)上得到一个向量\(\boldsymbol s=\mathcal A(M)\)，使得\(\mathcal H(\boldsymbol s)\)在F范数意义下距离\(M\)最近。其本质上是Hankel化的逆过程，通过称为去Hankel化(Hankelization)。通过最小二乘得到分量的显示解 \[ \boldsymbol s_i=\frac{1}{\beta-\alpha+1}\sum_{k=\alpha}^{\beta}M_{i-k+1,k} \] 其中\(\alpha=\max(1,i-m+1),\beta=\min(n,i)\)。如果矩阵\(M\)是秩1矩阵，即存在矩阵分解\(M=\boldsymbol u\boldsymbol v^T\)，则上述对角平均可简化为 \[ \mathcal A(M)=\mathcal A(\boldsymbol u\boldsymbol v^T)=D\mathcal T_p(\boldsymbol u)\boldsymbol v \] 其中\(N\times N\)对角矩阵\(D=\text{diag}(1,2^{-1},\ldots,\mu^{-1},\ldots,\mu^{-1},\ldots,2^{-1},1)\)，\(\mu=\min(m,n)\)。

截断奇异值分解的滤波器表示

对给定的输入信号\(\boldsymbol s_{in}\)的Hankel矩阵进行奇异值分解 \[ H=\mathcal H(\boldsymbol s_{\text{in}})=\sum_{i=1}^{n}\sigma_i \boldsymbol u_i \boldsymbol v_i^T \] 截断奇异值分解则保留前\(k\)个奇异值从而得到秩\(k\)矩阵\(H_k\)的矩阵\(H\)近似。下面以加权的形式表示 \[ H_k=\sum_{i=1}^{k}w_i\sigma_i \boldsymbol u_i \boldsymbol v_i^T \] 当权值\(w_i=1\)时，\(H_k\)为最小二乘逼近。当\(w_i=1-\frac{\sigma_{\text{noies}}^2}{\sigma_i^2}\)时，\(H_k\)为最小方差近似，其中\(\sigma_{\text{noies}}\)为白噪声的方差，可取为最小的奇异值。

接下来需要从秩\(k\)矩阵\(H_k\)重构出去噪信号，通过反对角平均即可得到输出结果。 \[ \begin{aligned} \boldsymbol s_{\text{out}}&=\mathcal A(H_k)\\ &=\mathcal A(\sum_{i=1}^{k}w_i\sigma_i \boldsymbol u_i \boldsymbol v_i^T)\\ &=\sum_{i=1}^{k}w_i\mathcal A(\sigma_i \boldsymbol u_i \boldsymbol v_i^T)\\ &=\sum_{i=1}^{k}w_i D\mathcal T_p(\sigma_i \boldsymbol u_i)\boldsymbol v_i\\ &=D\sum_{i=1}^{k}w_i \mathcal T_p(H \boldsymbol v_i)\boldsymbol v_i\\ &=D\sum_{i=1}^{k}w_i \mathcal H_p(H \boldsymbol v_i)(J\boldsymbol v_i)\\ &=D\sum_{i=1}^{k}w_i \mathcal H_p(\mathcal H(\boldsymbol s_{\text{in}}) \boldsymbol v_i)(J\boldsymbol v_i) \end{aligned} \] 记\(\boldsymbol s_i=\mathcal H_p(\mathcal H(\boldsymbol s_{\text{in}}) \boldsymbol v_i)(J\boldsymbol v_i)\)，则输出可表示为加权形式\(\boldsymbol s_{\text{out}}=D\sum_{i=1}^{k}w_i \boldsymbol s_i\)。

对于每个\(\boldsymbol s_i\)

• \(\mathcal H(\boldsymbol s_{\text{in}}) \boldsymbol v_i\)表示为输入\(\boldsymbol s_{\text{in}}\)经过由\(\boldsymbol v_i\)决定的FIR滤波器的输出结果
• \(\boldsymbol s_i\)表示为输入\(\mathcal H(\boldsymbol s_{\text{in}}) \boldsymbol v_i\)经过由\(J\boldsymbol v_i\)决定的FIR滤波器的输出结果
• 根据\(J\)可得两个滤波器的系数是逆序的，产生一个零相位的滤波器
• 滤波器\(\boldsymbol v_i\)和滤波器\(J\boldsymbol v_i\)是并行连接的分析(analysis)和合成(synthesis)滤波器对
• 由特征向量\(\boldsymbol v_i\)得到的滤波器与特征滤波器有着密切的联系

截断奇异值分解的滤波器图示

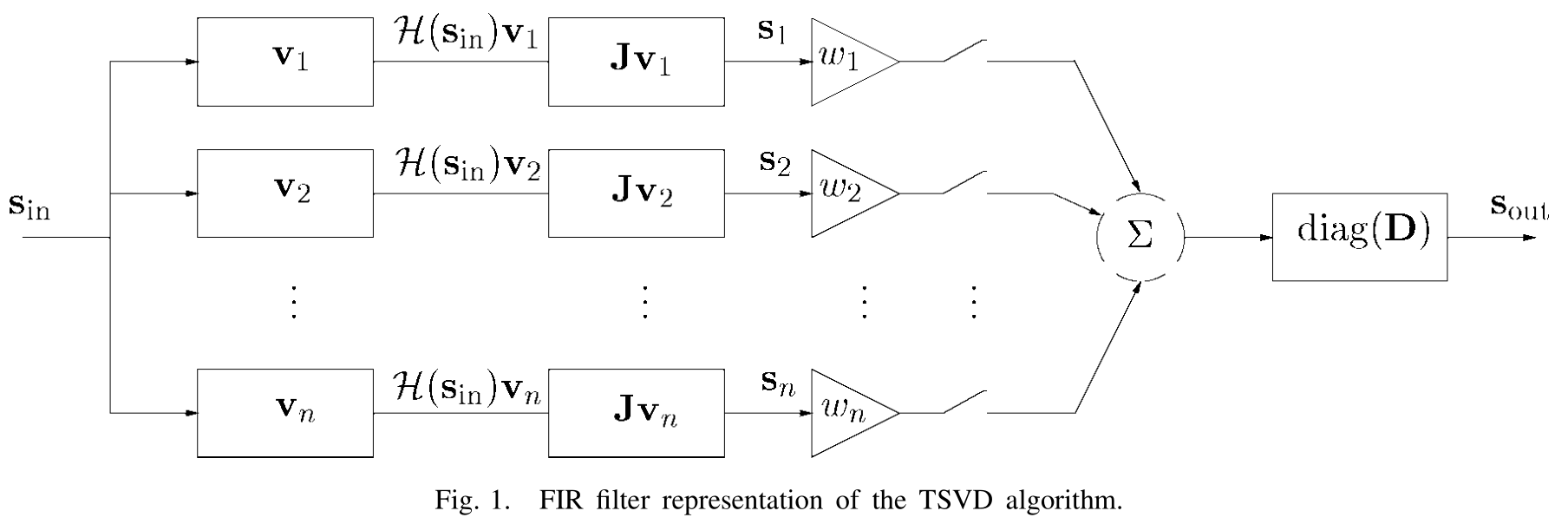
该示意图包含\(n\)条分支，分支按照奇异值大小降序排列，每个分支上设置了开关。

• 如果仅打开前\(k\)个开关，则得到截断奇异值分解
• 如果打开所有开关且设\(w_i=1\)，则得到传统的奇异值分解

截断商奇异值分解

上面的截断奇异值分解仅适用于高斯白噪声，而对于有色噪声(color)，预白化(prewhitening)和去白化(dewhitening)是非常常见的信号处理方法。下面则对商奇异值分解进行截断。

由广义的奇异值分解可知，矩阵对\((\mathcal H(\boldsymbol s_{\text{in}}),\mathcal H(\boldsymbol e))\)的商奇异值分解的结果为 \[ \mathcal H(\boldsymbol s_{\text{in}})=\sum_{i=1}^n\delta_i \hat {\boldsymbol u}_i\boldsymbol x_i^T,\mathcal H(\boldsymbol e)=\sum_{i=1}^n\mu_i \hat {\boldsymbol v}_i\boldsymbol x_i^T \] 其中\(\hat {\boldsymbol u}_i,\hat {\boldsymbol v}_i\)是正交向量，\(\boldsymbol x_i\)是线性无关的，\(\delta_i^2+\mu_i^2=1\)。商奇异值\(\{\frac{\delta_i}{\mu_i}\}\)是降序排列。当噪声是白噪声时，商奇异值分解退化到典型的奇异值分解。下面构造\(\mathcal H(\boldsymbol s_{\text{in}})\)的秩\(k\)近似矩阵 \[ Z_k=\sum_{i=1}^{k}w_i\delta_i \hat {\boldsymbol u}_i\boldsymbol x_i^T \] 类似于前面的截断奇异值分解，截断商奇异值分解的重构信号为 \[ \boldsymbol s_{\text{out}}=\mathcal A(Z_k)=D\sum_{i=1}^{k}w_i \mathcal H_p(\mathcal H(\boldsymbol s_{\text{in}}) \boldsymbol \theta_i)(J\boldsymbol x_i) \] 其中需要注意构造一个双正交的向量组\((\boldsymbol \theta_1,\ldots,\boldsymbol \theta_n)^T=(x_1,\ldots,x_n)^{-1}\)，即\(\boldsymbol \theta_i^Tx_j=1\)。由此可得等式\(H\boldsymbol \theta_i=\delta_i\hat {\boldsymbol u}_i\)。

截断商奇异值分解的滤波器图示

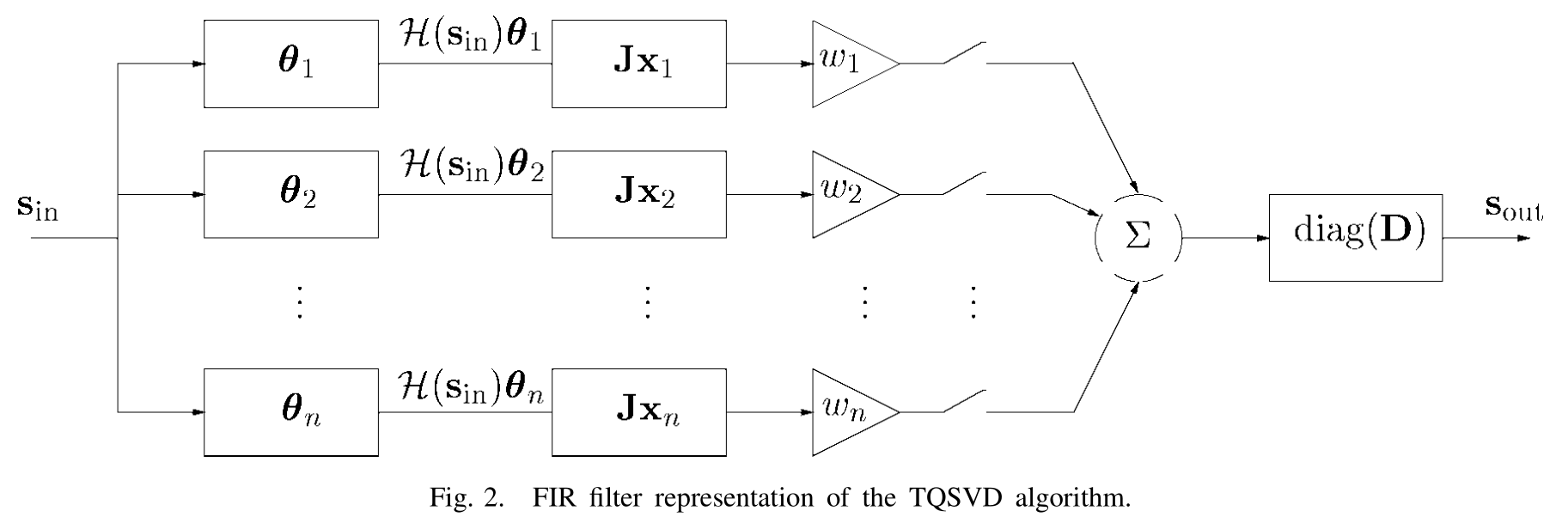
每个分支的滤波器由滤波器\(\boldsymbol \theta_i\)和滤波器\(J\boldsymbol x_i\)是并行连接，因此不再是零相位滤波器了。

References

1. Leles M C R , Cardoso A S , Moreira M G , et al. Frequency-domain characterization of Singular Spectrum Analysis eigenvectors[C]// IEEE International Symposium on Signal Processing & Information Technology. IEEE, 2016. ↩︎
2. Harris T J , Yuan H . Filtering and frequency interpretations of Singular Spectrum Analysis[J]. Physica D Nonlinear Phenomena, 2010, 239(20-22):1958-1967. ↩︎
3. Hansen P C , Jensen S H . FIR filter representations of reduced-rank noise reduction[J]. Signal Processing IEEE Transactions on, 1998, 46(6):1737-1741. ↩︎