介绍最近看的两篇基于\(\ell_1\)范数主成分分析(Principal Component Analysis, PCA)的文章^[1]\(^,\)^[2]

基于\(\ell_1\)范数的主成分分析

PCA简介

• 降维技术
• 数据可视化
• 人脸识别（特征脸，eigenface）
• 广泛应用

PCA优缺点

• 计算效率高（SVD）
• 对异常值不鲁棒

L2-PCA

传统的主成分分析L2 PCA的两个目的

• 最近重构性

\[ \min_W -\operatorname{tr}(W^TXX^TW)\quad \text{s.t.} W^TW = I \]

• 最大可分性

\[ \max_W \operatorname{tr}(W^TXX^TW)\quad \text{s.t.} W^TW = I \]

最小化误差和最大化方差在距离度量取L2-范数时是等价的，并可通过SVD来求解。从第一点看出PCA的本质是保证原样本点和投影重构的样本点距离服从高斯分布，其最小化可以去除高斯噪声 \[ \begin{aligned} E_2(W,V) &= \|X-WV\|_2^2 = \sum_{i=1}^n \|x_i - \sum_{k=1}^m w_k v_{ki}\|_2^2 \\ &= \sum_{i=1}^n \sum_{j=1}^d (x_{ji} - \sum_{k=1}^m w_{jk}v_{ki})^2 \end{aligned} \]

假设\(W\)固定，由投影定理可知，\(\min_V E_2(V)\quad \text{s.t.} W^TW = I\)的解是\(V=W^T X\)，这也可以从下面事实解释 \[ X=WV \iff V = W^TWV = W^TX \] 所以就有了如下等价问题 \[ \min \|X-WV\|_2 \iff \min \|X-WW^TX\|_2 \iff \min \|W^TX\|_2 \] L2 PCA对异常值和稀疏噪声效果很差，因此原始数据和投影之间的距离用拉普拉斯分布来代替高斯分布，根据极大似然估计提出L1 PCA。 \[ \begin{aligned} E_1(W,V) &= \|X-WV\|_1 = \sum_{i=1}^n \|x_i - \sum_{k=1}^m w_k v_{ki}\|_1 \\ &= \sum_{i=1}^n \sum_{j=1}^d |x_{ji} - \sum_{k=1}^m w_{jk}v_{ki}| \end{aligned} \] 由于L1范数不是旋转不变的，且等距曲面倾斜不利于获取最优的精确解。R1 PCA结合L2 PCA和L1 PCA来保证旋转不变性，但是对维度敏感。 \[ E_{R1}(W,V) = \|X-WV\|_{R1} = \sum_{i=1}^n (\sum_{j=1}^d (x_{ji} - \sum_{k=1}^m w_{jk}v_{ki})^2)^{\frac{1}{2}} \]

L1 PCA与R1 PCA的关系更像TV范数的关系：

• 各向同性TV范数

\[ \quad \left\| X_i \right\|_{\rm{TV}}^{\rm{iso}} = \left\| \sqrt{\left| \nabla_x X_i \right|^2 + \left|\nabla _y X_i \right|^2 }\right\|_1 \]

• 各项异性TV范数

\[ \left\| X_i \right\|_{\rm{TV}}^{\rm{ani}} = \left\| \nabla_x X_i \right\|_1 + \left\|\nabla _y X_i\right\|_1 \]

回到基于误差的子空间投影优化问题，其解可以通过对偶问题的SVD得到 \[ W^*=\arg\max_W\|W^TXX^TW\|_2 = \arg\max_W\|W^TX\|_2 \quad \text{s.t.} W^TW = I \] 注意，上式可解释为投影点\(W^TX\)的方差最大化，完成从协方差矩阵（二阶矩）到方差（一阶矩）的转化。此外，L2-PCA的对偶优化问题得到一个具有旋转不变性的子空间，但是对异常值不鲁棒。从下图可以看出，少量异常点严重影响投影的方向。

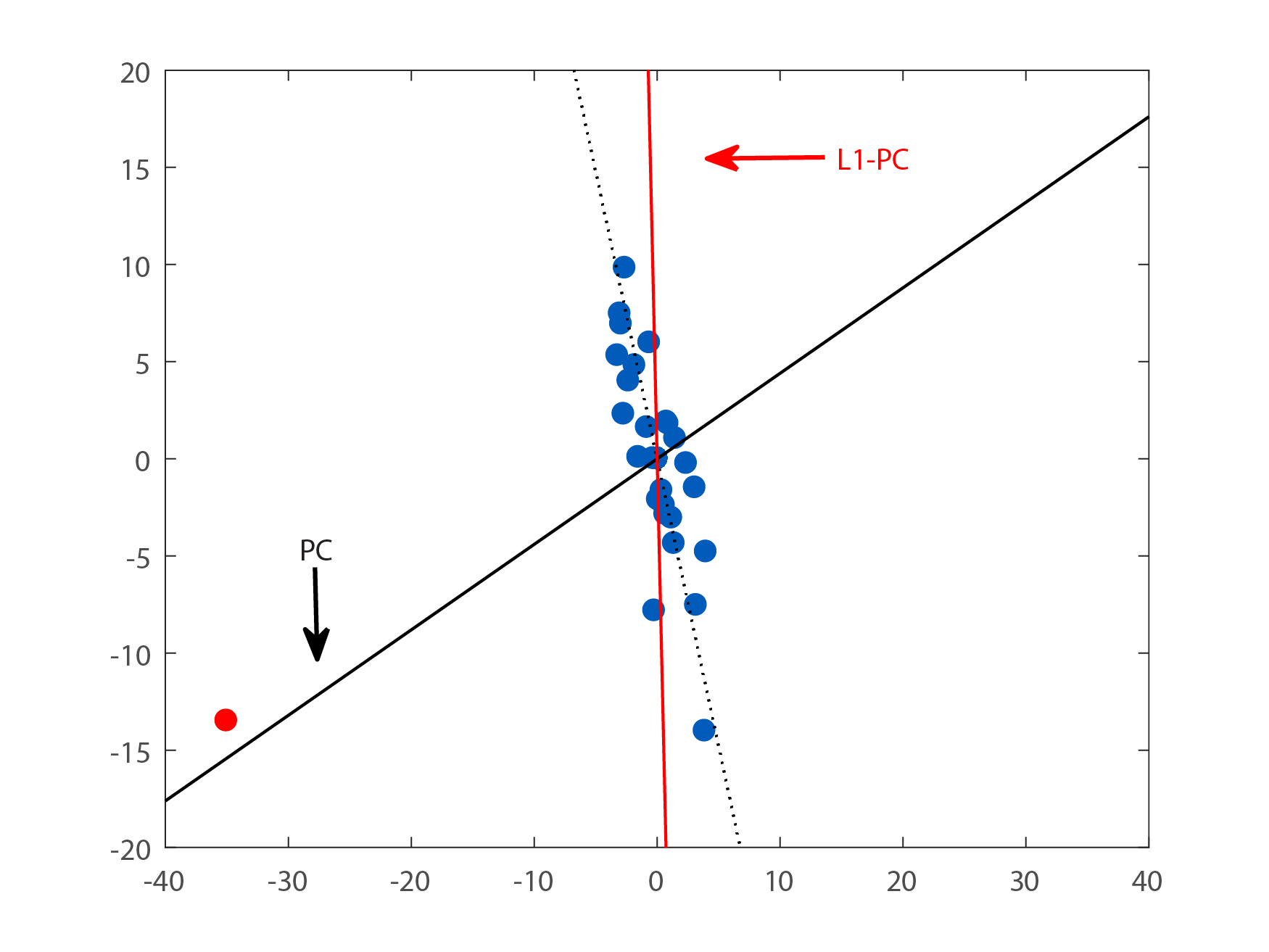
图片来源^[3]

L1-PCA

文献^[1]从方差角度考虑，用特征空间的最大化L1-范数方差来代替最大化基于L2-范数方差，以实现鲁棒和旋转不变的PCA。求解算法简单有效，且可证明达到局部最大解。具体优化模型PCA-L1如下： \[ W^* = \arg\max_W\|W^TX\|_1 = \arg\max_W \sum_{i=1}^n \sum_{k=1}^m | \sum_{j=1}^d w_{jk}x_{ji}| \quad \text{s.t.} W^TW = I \] PCA-L1模型比L1-PCA具备旋转不变性，比L2-PCA具备异常值的鲁棒性。该问题可以通过简化为\(m\)个子问题，利用贪婪算法求解 \[ w^* = \arg\max_w\|w^TX\|_1 = \arg\max_w \sum_{i=1}^n |w^Tx_i| \quad \text{s.t.} \|w\|_2 = I \]

1. 初始化：任取\(w(0)\)，单位化\(w(0)\leftarrow w(0)/\|w(0)\|_2\)，令\(t=0\)
2. 极性检查：若\(w^T(t)x_i<0\)，设\(p_i(t) = -1\)，否则\(p_i(t) = 1\)
3. 翻转和最大化：\(t\leftarrow t+1\)，\(w(t)=\sum_{i=1}^np_i(t-1)x_i\)，再单位化\(w(t)\leftarrow w(t)/\|w(t)\|_2\)
4. 判断收敛：

• 若\(w(t) \neq w(t-1)\)，到\((2)\)
• 若存在\(i\)使得\(w^T(t)x_i=0\)，设\(w(t)\leftarrow (w(t)+\Delta w)/\|w(t)+\Delta w\|_2\)，到\((2)\)，其中\(\Delta w\)为非零随机向量
• 否则\(w^* = w(t)\)，停止迭代

迭代过程中 \[ \begin{aligned} \sum_{i=1}^n |w^T(t) x_i| &= w^T(t)(\sum_{i=1}^n p_i(t) x_i) \\ & \geq w^T(t)(\sum_{i=1}^n p_i(t-1) x_i)\\ & \geq w^T(t-1)(\sum_{i=1}^n p_i(t-1) x_i)\\ & =\sum_{i=1}^n |w^T(t-1) x_i| \end{aligned} \]

• 第一个不等号是因为\(p_i(t)\)是\(w(t)\)保证\(p_i(t)w^T(t)x_i\geq0\)的最优极性（符号），但\(p_i(t-1)\)不是。

• 第二个不等号是因为\(\|w(t)\|_2=\|w(t-1)\|_2\)，因此与向量\(\sum_{i=1}^n p_i(t-1) x_i\)做乘法时向量夹角越小内积越大，平行时最优 \[ \frac{\sum_{i=1}^np_i(t-1)x_i}{\|\sum_{i=1}^np_i(t-1)x_i\|} \]

• 因此在这一个算法下目标函数是非减的。经过有限步以后可收敛到投影向量\(w^*\)，且目标函数在\(w^*\)处有一个局部极大值。

• 算法计算复杂度为\({\mathcal{O}}(nd)\times n_{it}\)，不依赖于原空间维度\(d\)，而依赖于样本数\(n\)。

• 注意，算法寻找的局部最大值并不一定是全局最大值，因此合适的初始值\(w(0)\)设置可以减少迭代数而增大全局最优解的求解概率。

• 回到第三步，投影向量是数据点\(x_i\)的线性组合，即\(w(t)\propto p_i(t-1)x_i\)，因此对旋转具有不变性。

值得注意的是，L1-PCA和L2-PCA算法所得到得子空间非常接近。

上面仅考虑了当\(m=1\)的特例，对于\(m>1\)的情况可以通过贪婪寻找算法。

投影向量的正交性由以下三点保证：

• \(w_j\)是样本\(X^j\)的线性组合，可视为由\(X^j\)张成的子空间

• \[ w_{j-1}^T X^j = w_{j-1}^T X^{j-1} - w_{j-1}^T w_{j-1} w_{j-1}^T X^{j-1} = 0 \]

• \(w_{j-1}\)与\(X^j\)正交，因此\(w_j\)与\(w_{j-1}\)正交。

PCA-L1小结

• 寻找在投影空间中最大化L1范数的投影。
• 被证明可找到一个局部最大值。
• 对异常值具有鲁棒性。
• 简单且易于实现。
• 迭代次数较少，相对较快。
• 迭代次数不取决于输入空间的大小。
• 相同的技术可以应用于其他特征提取算法

二值核范数最大化问题

对任意矩阵\(A\)，记\(\Phi(A)\)为L2范数意义下距离\(A\)最近的正交矩阵 \[ \Phi(A) = \arg\min_{W}\|A-W\|_F,\quad \text{s.t.} W^T W = I_n \] 若\(A=U_A \Sigma_A V_A^T\)，Procrustes定理表示\(\Phi(A) = U_A V_A^T\) 。若\(B_{\text{BNM}}^*\)是如下二值核范数最大化问题(binary nuclear-norm maximization, BNM)的精确解 \[ \max_{B \in \{\pm 1\}^{N \times K}} \|XB\|_*^2 \] 则L1-PCA问题 \[ \arg\max_W\|W^TX\|_1 \quad \text{s.t.} W^TW = I \] 的精确解为\(W_{\ell_1}^* = \Phi(XB_{\text{BNM}}^*)\)，反之，BNM的解也可由L1-PCA问题的精确解表示\(B_{\text{BNM}}^* = \textbf{sgn}(X^T W_{\ell_1}^*)\)，这是因为 \[ \|X^T W_{\ell_1}^*\|_1 = \|XB_{\text{BNM}}^*\|_* \]

算法

L1-PCA模型可通过以下两步法来解决

1. 求解二值核范数最大化问题来获得\(B_{\text{BNM}}^*\)
2. 通过对\(XB_{\text{BNM}}^*\)SVD来获得\(W_{\ell_1}^*\)

其中第一步可通过L1-BF算法解决

基于\(\ell_1\)范数的复值主成分分析

上面提到L1-PCA模型得实值优化问题如下： \[ Q_{l_1}^* = \arg\max_{Q \in \mathbb{R}^{D\times K}}\|Q^T X\|_1 \quad \text{s.t.} Q^T Q = I_k \] 对应的复值版本则为 \[ Q_{l_1}^* = \arg\max_{Q \in \mathbb{C}^{D\times K}}\|Q^H X\|_1 \quad \text{s.t.} Q^H Q = I_k \] 该问题是一个NP-hard问题，目前研究集中于近似求解或求次优解。文献^[2]给出一个很巧妙的算法。

复数方向\(\textbf{sgn}\)

任意复数可表示为模长和角度乘积，其中角度表示为 \[ \begin{aligned} \textbf{sgn}(a) &= e^{j \textbf{Arg}(a)} = tan^{-1}(\frac{\mathfrak I\{a\}}{\mathfrak R\{a\}}) = \frac{a}{|a|} \\ &= \arg\max_{b \in U} |b-a|= \arg\max_{b \in U} \mathfrak R\{b^H a\} \end{aligned} \] 矩阵的形式如下 \[ \textbf{sgn}(A) = \left[\begin{array}{ccc} \operatorname{sgn}\left(a_{1,1}\right) & \dots & \operatorname{sgn}\left(a_{1, n}\right) \\ \vdots & \ddots & \vdots \\ \operatorname{sgn}\left(a_{m, 1}\right) & \dots & \operatorname{sgn}\left(a_{m, n}\right) \end{array}\right] = \arg\max_{B \in U^{n \times m}} \mathfrak R\{BA\} \] 对应的最优值为矩阵的\(\ell_1\)范数，即 \[ \|A\|_1 = \max_{B \in U^{n \times m}} \mathfrak R\{BA\} = tr(\textbf{sgn}(A)^H A) \] 而核范数作为奇异值之和，也可表示为 \[ \|A\|_* = \max_{Q \in \mathbb{C}^{m\times n}}\mathfrak R\{ tr(Q^H A)\} \quad \text{s.t.} Q^H Q = I_n \] 记上式最大化的酉矩阵\(\textbf{unt}(A) = UV^H\)，则\(A\)有极分解 \[ A = \textbf{unt}(A)(A^H A)^{\frac{1}{2}} \]

单位模优化（重点）

\[ \begin{aligned} \max_{Q \in \mathbb{C}^{D\times K}}\|Q^H X\|_1 &= \max_{Q \in \mathbb{C}^{D\times K}} tr(\textbf{sgn}(Q^H X)^H Q^H X) \\ &= \max_{Q \in \mathbb{C}^{D\times K} B\in U^{N\times K}} \mathfrak R\{ tr(B Q^H X)\} \\ &= \max_{B\in U^{N\times K}}\|XB\|_* \end{aligned} \]

最优解对\((Q_{\ell_1}^*,B^*)\)存在如下关系 \[ \begin{aligned} Q_{\ell_1}^*&=\textbf{unt}(XB^*)=\textbf{unt}(X\textbf{sgn}(X^H Q_{\ell_1}^*))\\ B^* &= \textbf{sgn}(X^H Q_{\ell_1}^*)= \textbf{sgn}(X^H \textbf{unt}(XB^*)) \end{aligned} \]

case 低秩矩阵

当\(rank(X)<D\)时，对于SVD\(X=U_r S_r V_r^H\)，有 \[ \begin{aligned} \|XB\|_* &= \|U_r S_r V_r^H B\|_* = tr((U_r S_r V_r^H B)^H(U_r S_r V_r^H B)^{\frac{1}{2}})\\ &= tr((B^H V_r^H S_r^H S_r V_r^H B)^{\frac{1}{2}}) = \|S_r V_r^H B\|_* \end{aligned} \] 记\(Y = S_r V_r^H\)，\(\hat Q _{\ell_1}^* = \arg\min_{Q \in \mathbb{C}^{r\times K}} \|Q^HH\|_1 \quad \text{s.t.} Q^H Q = I_k\)，则有

\[ \begin{aligned} U_r Y B^* = U_r \textbf{unt}(YB^*) \cdot (B^H V_r^H S_r^H S_r V_r^H B)^{\frac{1}{2}} \\ = XB^* = \textbf{unt}(XB^*) \cdot (B^H V_r^H S_r^H S_r V_r^H B)^{\frac{1}{2}} \end{aligned} \]

\[ \textbf{unt}(XB^*) = U_r \textbf{unt}(YB^*) \]

\[ Q _{\ell_1}^* = U_r \hat Q _{\ell_1}^* \]

\[ \|(Q _{\ell_1}^*)^H X\|_1 = \|XB^*\|_1 = \|YB^*\|_1 = \|(Q _{\ell_1}^*)^H Y\|_1 \]

case 单成分

\[ \begin{aligned} \max_{q \in \mathbb{C}^{D\times 1},\|q\|_2 = 1} \|q^H X\|_1 & = \max_{b \in U^{N \times 1}} \|Xb\|_*= \max_{b \in U^{N \times 1}} \|Xb\|_2\\ & = \max_{b \in U^{N \times 1}} (b^H X^H X b)^{\frac{1}{2}} \end{aligned} \]

该单位模二次优化问题的解 \[ q_{\ell_1}^* = \textbf{unt}(Xb^*) = Xb^*\|Xb^*\|_2^{-1} \]

\[ b^* = \textbf{sgn}(X^H q_{\ell_1}^*) = \textbf{sgn}(X^H \textbf{unt}(Xb^*)) =\textbf{sgn}(X^H Xb^*) \]

因为\(\textbf{sgn}(X^H Xb^*)\)满足\(\|Xb\|_2\)的鞍点，上式不是局部最优解的充分条件。下面提供了一个更强的最优性条件且满足局部最优解的充要性。

记\(\omega(b) = \bar b \odot (X^H X b)\)，则单模向量\(b\)满足局部最优性的充要条件为 \[ \|x_n\|_2^2 \leq \omega_n(b) \in \mathbb R \quad \forall n \in \{1,\dots, N\} \] 不等式引导符号函数的对应结果为 \[ b = \textbf{sgn}((X^H X- \textbf{diag}(\|x_1\|_2^2,\dots,\|x_N\|_2^2)) b) \] \(\textbf{sgn}(X^H Xb^*)\)与该式的差异在于\(\omega(\cdot)\)的取值：前者仅保证\(\omega_n(b^*)>0\)；而后者进一步保证\(\omega_n(b^*)\geq\|x_n\|_2^2>0\)。

复L1-PCA算法

• 算法1

\[ B^{(i)}= \textbf{sgn}(X^H \textbf{unt}(X B^{(i-1)})) \]

收敛性 \[ \begin{aligned} \|X B^{(i)}\|_* & = \max_Q \mathfrak R\{ tr(Q^H XB^{(i)})\} \\ & \geq \mathfrak R\{ tr(\textbf{unt}(XB^{(i-1)}))^H XB^{(i)}\}\\ & = \mathfrak R\{ tr(\textbf{unt}(XB^{(i-1)}))^H X \textbf{sgn}(X^H \textbf{unt}(X B^{(i-1)}))\}\\ & = \max_B \mathfrak R\{ tr(\textbf{unt}(XB^{(i-1)}))^H X B'\}\\ & \geq \mathfrak R\{ tr(\textbf{unt}(XB^{(i-1)}))^H X B^{(i-1)}\} = \|X B^{(i-1)}\|_* \end{aligned} \]

• 算法2

\[ b^{(i)} = \textbf{sgn}((X^H X- \textbf{diag}(\|x_1\|_2^2,\dots,\|x_N\|_2^2)) b^{(i-1)}) \]

收敛性 \[ \begin{aligned} \left\|\mathbf{A}_{d} \mathbf{b}^{(i)}\right\|_{1} &=\max _{\mathbf{b} \in U^{N \times 1}} \Re\left\{\mathbf{b}^{H} \mathbf{A}_{d} \mathbf{b}^{(i)}\right\} \\ & \geq \Re\left\{\mathbf{b}^{(i-1)^{H}} \mathbf{A}_{d} \mathbf{b}^{(i)}\right\} \\ &=\Re\left\{\mathbf{b}^{(i-1)^{H}} \mathbf{A}_{d} \operatorname{sgn}\left(\mathbf{A}_{d} \mathbf{b}^{(i-1)}\right)\right\} \\ &=\left\|\mathbf{A}_{d} \mathbf{b}^{(i-1)}\right\|_{1} \end{aligned} \]

总结

改变传统问题的范数是一直研究思路，第一篇文章将PCA的\(\ell_2\)改为\(\ell_1\)，而第二篇推进至复数域中，并利用符号函数联系\(\ell_1\)和核范数，通过巧妙转化 \[ \max_{Q \in \mathbb{C}^{D\times K}}\|Q^H X\|_1 = \max_{B\in U^{N\times K}}\|XB\|_* \] 将原问题改为单模优化问题。

参考文献

1. Kwak N. Principal Component Analysis Based on L1-Norm Maximization[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(9): 1672-1680. ↩︎
2. Tsagkarakis N, Markopoulos P P, Sklivanitis G, et al. L1-Norm Principal-Component Analysis of Complex Data[J]. IEEE Transactions on Signal Processing, 2018, 66(12): 3256-3267. ↩︎
3. L1-norm principal component analysis ↩︎