介绍最近看的基于\(\ell_p\)范数主成分分析(Principal Component Analysis, PCA)的文章^[1]

基于\(\ell_p\)范数的主成分分析

• \(\ell_2\)-PCA

\[ F_2 (W) = \frac{1}{2}\sum_{i=1}^{N} \|W^T x_i\|_2^2 = \frac{1}{2} tr(W^T XX^T W) \]

• \(\ell_1\)-PCA

\[ F_1 (W) = \sum_{i=1}^{N} \|W^T x_i\|_1 = \sum_{i=1}^{N} \sum_{j=1}^{m} |w_j^T x_i| \]

• \(\ell_p\)-PCA

\[ F_p (W) = \frac{1}{p} \sum_{i=1}^{N} \|W^T x_i\|_p^p = \frac{1}{p} \sum_{i=1}^{N} \sum_{j=1}^{m} |w_j^T x_i|^p \]

求解算法(\(m=1\))

梯度下降

对应模型 \[ w^* = \arg\min_w F_p(w) = \arg\min_w \frac{1}{p} \sum_{i=1}^{N} |w^T x_i|^p \quad \text{s.t.} w^Tw = 1 \]

记\(a_i = w^T x_i\)，则 \(F_p (w) = \frac{1}{p} \sum_{i=1}^{N} (\text{sgn}(a_i)a_i)^p\)对\(w\)的梯度为 \[ \begin{aligned} \nabla_{w} &=\frac{d F_{p}(w)}{d w}=\sum_{i=1}^{N} \frac{d F_{p}(w)}{d a_{i}} \frac{d a_{i}}{d w} \\ &=\sum_{i=1}^{N}\left[\text{sgn}\left(a_{i}\right) a_{i}\right]^{p-1}\left[\text{sgn}^{\prime}\left(a_{i}\right) a_{i}+\text{sgn}\left(a_{i}\right)\right] x_{i} \\ &=\sum_{i=1}^{N} \text{sgn}^{\prime}\left(a_{i}\right) \text{sgn}^{p-1}\left(a_{i}\right) a_{i}^{p} x_{i}+\sum_{i=1}^{N} \text{sgn}^{p}\left(a_{i}\right) a_{i}^{p-1} x_{i} \\ &=2 \sum_{i=1}^{N} \delta\left(a_{i}\right) \text{sgn}^{p-1}\left(a_{i}\right) a_{i}^{p} x_{i}+\sum_{i=1}^{N} \text{sgn}\left(a_{i}\right)\left|a_{i}\right|^{p-1} x_{i} \end{aligned} \] 当\(a_i = w^T x_i \neq 0\)，则梯度的第一项为0，即 \[ \nabla_{w} = \sum_{i=1}^{N} \text{sgn}\left(w^T x_i\right)\left|w^T x_i\right|^{p-1} x_{i} \] 若\(p > 1\)，即使存在奇异点(\(w^T x_i = 0\))，第一项也为0，其梯度也是良定义的(见上式)。而当\(p < 1\)时需要对\(w\)进行扰动来避免奇异情况(\(w^T x_i = 0\))。

该问题可以通过最速下降法来迭代求解。

• 初值选取
  • \(\ell_2\)-PCA的结果
  • 具有最大范数的样本方向
• 学习率控制收敛速率，\(\alpha = \frac{0.1}{N}\)
• step 2 避免当\(p \leq 1\)时的奇异情况
• step 5 保证规范化\(\|w\|_2 = 1\)

基于梯度下降的PCA-Lp算法

梯度正交向量

\[ \begin{aligned} \nabla_{w}^{\perp} &=\nabla_{w}-w\left(w^{T} \nabla_{w}\right)=\left(I_{d}-w w^{T}\right) \nabla_{w} \\ &=\left(I_{d}-w w^{T}\right) \sum_{i=1}^{N} \text{sgn}\left(w^{T} x_{i}\right)\left|w^{T} x_{i}\right|^{p-1} x_{i} \end{aligned} \]

令 \[ c_i = \text{sgn}\left(w^{T} x_{i}\right)\left|w^{T} x_{i}\right|^{p-1}, v_i = \left(I_{d}-w w^{T}\right) x_{i}, f_i = c_i v_i \] 则 \[ \nabla_{w}^{\perp} = \sum_{i=1}^{N} c_i v_i = \sum_{i=1}^{N} f_i \]

• \(a_i = |w^T x_i|,v_i = x_i - w(w^T x_i)\)
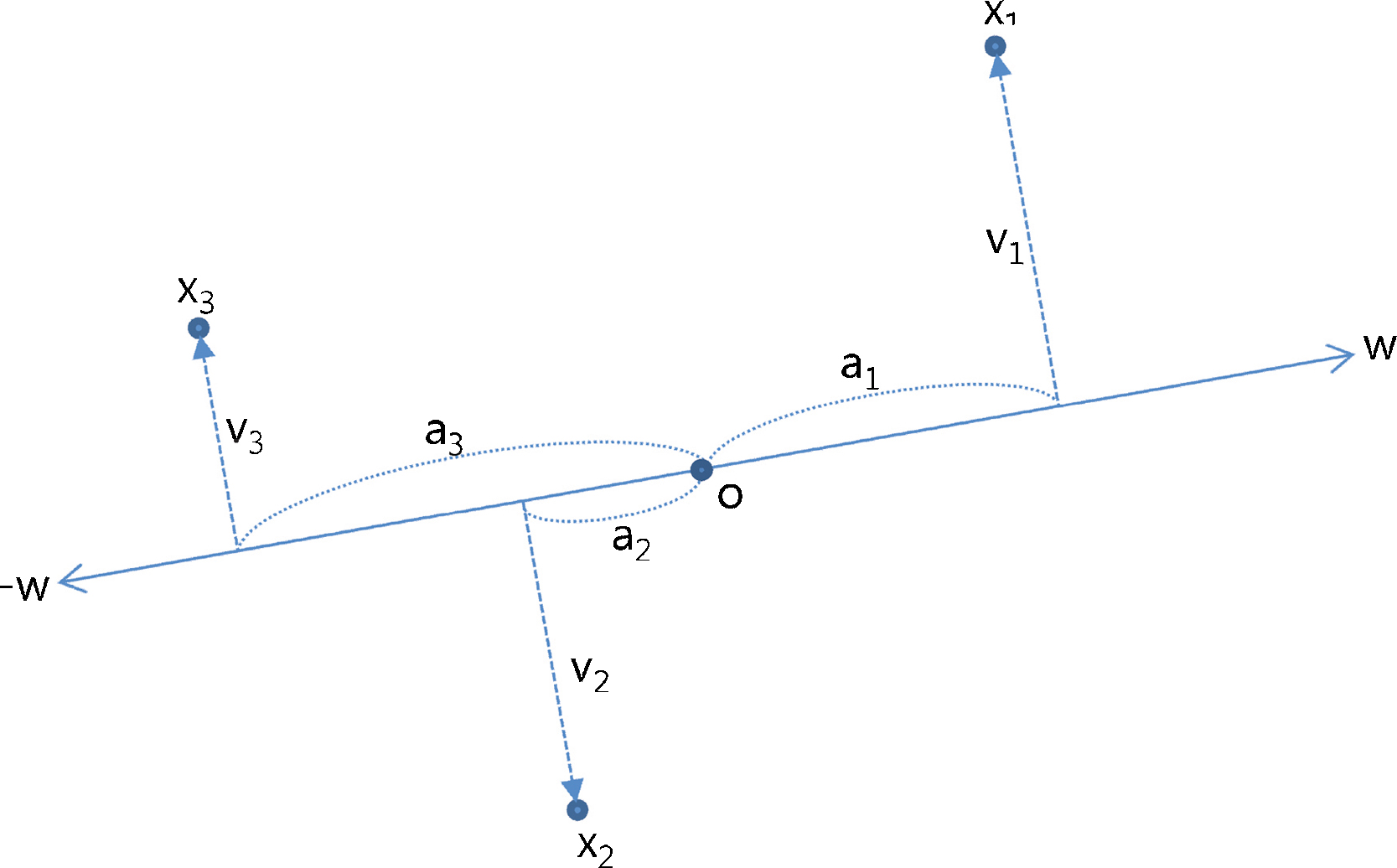
• \(w\)过原点\(O\)旋转
• 每一个样本 \(x_i\) 对 \(w\) 施加一个正交的力 \(f_i\)
  • 当 \(w^T x_i > 0\) ，点 \(x_i\) 对 \(w\) 产生拉力
  • 当 \(w^T x_i < 0\) ，点 \(x_i\) 对 \(w\) 产生推力，反之对 \(-w\) 产生拉力
  • 力的大小为\(|f_i| = a_i^{p-1}|v_i|\)
    • \(p=2\)时，\(|f_i| = a_i|v_i|\)，力收到两方面的乘积影响(拟合性)
    • \(p=1\)时，\(|f_i| = |v_i|\)，力只收到一方面的乘积影响(鲁棒性)
    • \(p<1\)时，\(|f_i| = (\frac{|v_i|}{a_i})^{1-p}|v_i|^p\)，\(a_i\)对力产生负影响，从而降低异常值的干扰
    • \(p \to 0\)时，\(|f_i| = \frac{|v_i|}{a_i}\)

传统PCA联系

当\(p = 2\)时 \[ \nabla_{w} = \sum_{i=1}^{N} \text{sgn}\left(w^T x_i\right)\left|w^T x_i\right|^{p-1} x_{i} = \sum_{i=1}^{N} x_{i} x_i^T w \]

\[ \nabla_{w}^{\perp} =\left(I_{d}-w w^{T}\right) \sum_{i=1}^{N} \text{sgn}\left(w^{T} x_{i}\right)\left|w^{T} x_{i}\right|^{p-1} x_{i} = \left(I_{d}-w w^{T}\right) XX^T w \]

因此优化问题可以通过协方差矩阵的特征值分解解决。而梯度正交向量有如下性质： \[ \nabla_{w}^{\perp} = 0 \iff \nabla_{w} = XX^T w \]

拉格朗日乘子法

约束优化问题转化为如下 \[ L(w, \lambda ) = F_p(w) + \lambda (w^T w - 1) \] 令拉格朗日函数导数为0可得最优解的必要性 \[ \frac{dL(w,\lambda)}{dw} = \nabla_w + \lambda w = 0 \] 可得\(w\)与梯度\(\nabla_w\)平行，又\(\|w\|_2=1\)，因此可对\(w\)直接更新 \[ w \leftarrow \frac{\nabla_w}{\|\nabla_w\|_2} \] 通常情况下，这种令导数为零方法取到的不仅是最大值，也有可能是最小值。因此在\(\ell_p\)-PCA里，对\(p \geq 1\)，由\(F_p\)的凸性可得该迭代下的目标函数非减。 \[ F_p(w^{k+1}) \geq F_p(w^{k}) + \nabla_w^T (w^{k+1} - w^{k}) \geq F_p(w^{k}) \] 第二个不等号是因为\(\|w^{k+1}\|_2 = \|w^{k}\|_2 = 1\)且\(w^{k+1}\)平行于\(\nabla_w\)，\(\nabla_w^T w^{k+1} = 1\)。

基于Lagrangian乘子法的PCA-Lp算法

求解算法(\(m>1\))

贪婪算法（近似求解）

• 往往求得局部最优解，而不是全局最优解

非贪婪解

对目标函数求梯度 \[ \nabla_W = \frac{dF_p(W)}{dW} = [\nabla_{w_1},\dots,\nabla_{w_m}] \] 对应的拉格朗日函数为 \[ L(W, \Gamma_m ) = F_p(W) + tr(\Gamma_m^T (W^T W - I_m)) \] 同样的，设导数为0，即 \[ \frac{dL(W, \Gamma_m )}{dW} = \nabla_W + 2W\Gamma_m = 0 \] 迭代不能再是简单的赋值，需满足正交约束，因此考虑如下优化问题 \[ W^* = \arg\max_Q tr(Q^T \nabla_W) \quad \text{s.t.} Q^T Q = I_m \] 设\(\nabla_W\)的SVD分解为\(\nabla_W = U\Lambda V^T\)，记\(Z = V^T Q^T U\)，得\(ZZ^T = I_d,z_{ii}\leq 1\)。因此 \[ \begin{aligned} tr(Q^T \nabla_W) &= tr(Q^T U\Lambda V^T) = tr(\Lambda V^T Q^T U) \\ &= tr(\Lambda Z) = \sum_i \lambda_{ii}z_{ii} \leq \sum_i \lambda_{ii} \end{aligned} \] 取等号时当且仅当\(z_{ii} = 1\)，此时\(Z = [I_m | 0]\)，最优解 \[ W^* = U Z^T V^T = U [I_m | 0]^T V^T \]

参考文献

1. Kwak N. Principal component analysis by Lp-norm maximization. IEEE Trans Cybern. 2014;44(5):594-609. ↩︎