写在前面

介绍稀疏主成分分析算法(Sparse Principal Component Analysis)^[1]

线性回归模型

PCA

The Elements of Statistical Learning 14.5里通过线性拟合的角度阐述了主成分的概念，这在SPCA里起到一个辅助理解的作用，在此进行补充。

\(\mathbb R^p\)空间中数据基\({x_1,x_2,\ldots,x_N}\)的主成分是秩为\(k(<p)\)的最佳线性近似序列（正交投影得到线性子空间） \[ f(\lambda)= \mu + V_k \lambda \] 通过重构误差最小二乘对原始数据进行拟合操作 \[ \min_{\mu,\lambda_i,V_k} \sum_{i=1}^N \|x_i - \mu- V_k \lambda_i\|^2 \] 令目标函数对\(\mu\)和\(\lambda_i\)的偏导为\(0\)可得 \[ \hat\mu = \bar x, \quad\hat\lambda = V_k^T(x_i-\bar x) \] 同时实现会对数据进行去均值化处理，即\(\bar x = 0\)，因此问题转化为对正交矩阵\(V_q\)优化 \[ \min_{V_k} \sum_{i=1}^N \|x_i - V_k V_k^Tx_i\|^2 \] 其中\(H_{k\times k} = V_k V_k^T\)为投影矩阵，并将点\(x_i\)映射至秩为\(k\)的重构点\(H_{k\times k} x_i\)，正交投影后的空间是由矩阵\(V_k\)的列所张成的子空间。

Lasso

在最小二乘的惩罚下添加对回归系数的\(\ell_1\)范数的约束 \[ \hat\beta_{\text{lasso}} = \arg\min_\beta \|Y - \sum_{j=1}^p X_j \beta_j\|^2 + \lambda \sum_{j=1}^p |\beta_j| \]

• 可通过最小角度回归LARS算法高效求解。

• 不适于样本少而维数高的变量选择，回归系数至多有\(n\)个非零项，这是因为凸优化问题的性质。

• 除非系数的\(\ell_1\)范数的边界小于某个值(由权衡参数\(\lambda\)确定)，否则Lasso不是良定义的(well-defined)。

• Lasso无法进行分组变量(grouped variables)选择，它倾向于从组中选择一个变量，而忽略其他变量。

Elastic Net

为了利用所有变量的信息，对岭回归和lasso进行凸组合 \[ \begin{aligned} \hat\beta_{\text{en}} = (1+\lambda_2)&\arg\min_\beta \|Y - \sum_{j=1}^p X_j \beta_j\|^2 \\ &+ \lambda_2 \sum_{j=1}^p |\beta_j|^2 + \lambda_1 \sum_{j=1}^p |\beta_j| \end{aligned} \]

• LARS-EN算法高效求解。
• 当\(\lambda_2 = 0\)时，Elastic Net退化为Lasso。
• 引入的二次项
  • 去除变量选择个数的限制，即适合样本少而维数高的情况
  • 有利于分组变量选择(grouping effect)
  • 稳定了\(\ell_1\)正则化的路径

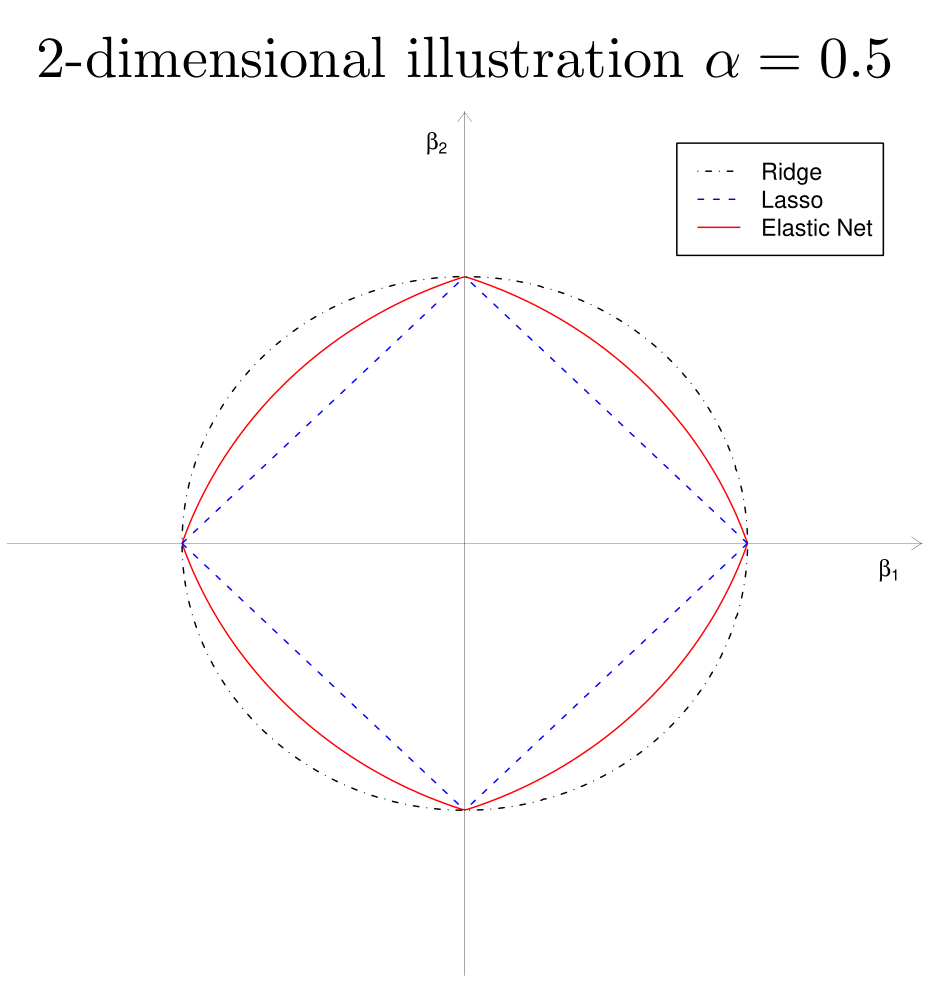
Elastic Net 正则化的几何性质

\[ J(\beta) = \alpha \|\beta\|^2 + (1 - \alpha)\|\beta\|_1 \leq t \]

• 顶点的奇异性（sparsity）
• 严格凸的边，凸度的强度随\(\alpha\)而变化（grouping）

稀疏主成分分析(SPCA)

主成分的岭回归

从PCA出发\(\mathrm X = \mathrm U \mathrm D \mathrm V^T\)，对主成分\(Z_i = U_i D_{ii}\)进行简单的岭回归 \[ \hat\beta_{\text{ridge}} = \arg\min_\beta \|Z_i -\mathrm X\beta\|^2 + \lambda \|\beta\|^2 \] 则归一化的系数\(\hat v = \frac{\hat\beta_{\text{ridge}}}{\|\hat\beta_{\text{ridge}}\|}\)与因子载荷相等，即\(\hat v = V_i\)。这表明奇异值分解得到右奇异向量与主成分的岭回归有潜在的关系，这一结论也不难证明。

由\(\mathrm X^T \mathrm X = \mathrm V \mathrm D^2 \mathrm V^T\)和岭回归的显示表达式 \[ \begin{aligned} \hat\beta_{\text{ridge}} &= (\mathrm X^T \mathrm X + \lambda \mathrm I)^{-1} \mathrm X^T (\mathrm X \mathrm V_i)\\ &= \frac{D_{ii}^2}{D_{ii}^2 + \lambda}\mathrm V_i \end{aligned} \]

稀疏近似

下面在岭回归的基础上加上\(\ell_1\)正则化得到去除倍数的Elastic Net \[ \arg\min_\beta \|Z_i -\mathrm X\beta\|^2 + \lambda \|\beta\|^2 + \lambda_1 \|\beta\|_1 \] 对得到的结果单位化\(\hat V_1 = \frac{\hat\beta}{\|\hat\beta\|}\)并称为右奇异向量\(V_i\)的近似，称\(\mathrm X \hat V_1\)为第\(i\)个主成分的近似。显然，\(\lambda_1\)越大，得到的\(\hat\beta\)越稀疏，因此\(\hat V_1\)越稀疏。

岭回归

考虑一个岭回归问题 \[ \hat \beta = \arg\min_\beta \|\mathrm y-\mathrm X\beta\|^2 + \lambda \|\beta\|^2 \] 设目标函数的导数为\(0\)可得最优解的必要条件 \[ \begin{aligned} &-\mathrm X^T (\mathrm y-\mathrm X\hat\beta) + \lambda \hat\beta = 0 \\ \Rightarrow\quad &\hat\beta = (\mathrm X^T\mathrm X + \lambda \mathrm I)^{-1}\mathrm X^Ty \end{aligned} \] 因此目标函数 \[ \begin{aligned} & \|\mathrm y-\mathrm X\hat\beta\|^2 + \lambda \|\hat\beta\|^2\\ & = (\mathrm y-\mathrm X\hat\beta)^T(\mathrm y-\mathrm X\hat\beta) + \lambda \hat\beta^T\hat\beta\\ & = (\mathrm y-\mathrm X\hat\beta)^T\mathrm y -(\mathrm y-\mathrm X\hat\beta)^T\mathrm X\hat\beta + \mathrm X\hat\beta)^T\mathrm X\hat\beta \\ & = \mathrm y^T(\mathrm I - \mathrm X(\mathrm X^T +\lambda \mathrm I)^{-1}\mathrm X^T)\mathrm y \end{aligned} \] 记岭回归算子\(\mathrm S_\lambda = \mathrm X(\mathrm X^T +\lambda \mathrm I)^{-1}\mathrm X^T\)，则满足\(\mathrm X\hat\beta = \mathrm S_\lambda \mathrm y\) 。

PCA重铸为回归模型

上面的优化问题都依赖PCA的结果，下面提出独立于SVD分解主成分的优化问题，建立PCA模型与回归型问题的联系。

首先考虑单个主成分。以第一个主成分为例，对任意\(\lambda > 0\) \[ \begin{aligned} (\hat \alpha, \hat \beta) = &\arg\min_{\alpha,\beta} \sum_{i=1}^n \|\mathrm x_i - \alpha\beta^T \mathrm x_i \|^2 + \lambda \|\beta\|^2 \\ &\text{s.t.} \|\alpha\|^2 = 1 \end{aligned} \] 则\(\hat\beta \propto V_1\)。这一结论的矩阵版本可以同时获得所有的主成分。记 \[ \mathrm A _{p \times k} = [\alpha_1, \ldots, \alpha_k], \mathrm B_{p \times k} = [\beta_1, \ldots, \beta_k] \] 对任意\(\lambda > 0\) \[ \begin{aligned} (\mathrm{\hat A}, \mathrm{\hat B}) =& \arg\min_{\mathrm A,\mathrm B} \sum_{i=1}^n \|\mathrm x_i - \mathrm A\mathrm B^T \mathrm x_i \|^2 \\ &+ \lambda \sum_{j=1}^k\|\beta_j\|^2 \quad \text{s.t.} \mathrm A^T \mathrm A = \mathrm I_{k \times k} \end{aligned} \] 则\(\hat\beta_j \propto V_j\)。

显然，令\(\mathrm B = \mathrm A\)，则\(\sum_{i=1}^n \|\mathrm x_i - \mathrm A\mathrm B^T \mathrm x_i \|^2 = \sum_{i=1}^n \|\mathrm x_i - \mathrm A\mathrm A^T \mathrm x_i \|^2\)，这是一个典型的基于重构误差的PCA模型。由于酉阵不改变矩阵的\(\ell_2\)范数，但半酉阵不具备这一性质，因此需要对\(\mathrm A\)补全为\([\mathrm A; \mathrm A_\bot]\)，其中\(\mathrm A_\bot\)是与\(\mathrm A\)正交的半酉阵。 \[ \begin{aligned} &\sum_{i=1}^n \|\mathrm x_i - \mathrm A\mathrm B^T \mathrm x_i \|^2 \\ =& \|\mathrm X - \mathrm X \mathrm B \mathrm A^T\|^2\\ =& \|(\mathrm X - \mathrm X \mathrm B \mathrm A^T)[\mathrm A; \mathrm A_\bot]\|^2\\ =& \|(\mathrm X - \mathrm X \mathrm B \mathrm A^T)\mathrm A_\bot\|^2 + \|(\mathrm X - \mathrm X \mathrm B \mathrm A^T)\mathrm A\|^2\\ =& \|\mathrm X \mathrm A_\bot\|^2 + \|\mathrm X \mathrm A- \mathrm X \mathrm B \|^2\\ =& \|\mathrm X \mathrm A_\bot\|^2 + \sum_{j=1}^k\|\mathrm X \alpha_j- \mathrm X \beta_j \|^2\\ \end{aligned} \]

• 若矩阵\(\mathrm A\)固定，上述优化问题转化为\(k\)个岭回归问题

\[ \arg\min_{\mathrm B} \sum_{j=1}^k\|\mathrm X \alpha_j- \mathrm X \beta_j \|^2 + \lambda \|\beta_j\|^2 \]

由岭回归的显示解可得 \[ \mathrm {\hat B} = (\mathrm X^T\mathrm X + \lambda \mathrm I)^{-1}\mathrm X^T \mathrm X \mathrm A \]

• 固定矩阵\(\mathrm {\hat B}\)，目标函数关于变量\(\mathrm A\)的优化问题为

\[ \begin{aligned} &\arg\min_{\mathrm A}\|\mathrm X - \mathrm X \mathrm {\hat B} \mathrm A^T\|^2 + \lambda \sum_{j=1}^k\|\beta_j\|^2 \\ =& \arg\min_{\mathrm A}\text{tr}(\mathrm X^T \mathrm X) - \text{tr}(\mathrm A^T\mathrm X^T \mathrm S_\lambda \mathrm X\mathrm A)\\ =& \arg\max_{\mathrm A} \text{tr}(\mathrm A^T\mathrm X^T \mathrm S_\lambda \mathrm X\mathrm A) \quad \text{s.t.} \mathrm A^T \mathrm A = \mathrm I_{k \times k} \end{aligned} \]

因此\(\mathrm A\)为矩阵\(\mathrm X^T \mathrm S_\lambda \mathrm X\)的最大的\(k\)个特征值对应的特征向量。设\(\mathrm X = \mathrm U \mathrm D \mathrm V^T\)，则 \[ \mathrm X^T \mathrm S_\lambda \mathrm X = \mathrm V\mathrm D^2(\mathrm D^2+\lambda \mathrm I)^{-1}\mathrm D^2 \mathrm V^T \] 故\(\mathrm {\hat A} = \mathrm V[, 1:k]\)，这也将岭回归与PCA建立联系，而\([\mathrm A; \mathrm A_\bot] = \mathrm V\)。

• 返回去再看\(\mathrm {\hat B}\)与\(\mathrm V\)成比例关系。

\[ \hat \beta_j = (\mathrm X^T\mathrm X + \lambda \mathrm I)^{-1}\mathrm X^T \mathrm X V_j \propto V_j \]

岭回归与Lasso的组合:SPCA

\[ \begin{aligned} (\mathrm{\hat A}, \mathrm{\hat B}) = &\arg\min_{\mathrm A,\mathrm B} \sum_{i=1}^n \|\mathrm x_i - \mathrm A\mathrm B^T \mathrm x_i \|^2 + \lambda \sum_{j=1}^k\|\beta_j\|^2\\ & + \sum_{j=1}^k\lambda_{1,j}\|\beta_j\|_1 \quad \text{s.t.} \mathrm A^T \mathrm A = \mathrm I_{k \times k} \end{aligned} \]

该问题对两个变量不是凸的，但对单个变量而固定另一个变量时是凸的，因此采用交替方式迭代。

• 给定\(\mathrm A\)更新\(\mathrm B\)

\[ \begin{aligned} &\arg\min_{\mathrm B} \sum_{i=1}^n \|\mathrm x_i - \mathrm A\mathrm B^T \mathrm x_i \|^2 \\ \iff &\arg\min_{\mathrm B} \sum_{j=1}^k \|\mathrm X \alpha_j - \mathrm X\beta_j\|^2 \end{aligned} \]

令\(Y_j^* = \mathrm X \alpha_j\)，优化问题可转化为\(k\)个Elastic net 子问题 \[ \begin{aligned} \hat \beta_j =& \arg\min_\beta \|Y_j^* - \mathrm X\beta\|^2 + \lambda \|\beta\|^2 + \lambda_{1,j}\|\beta\|_1\\ =& \arg\min_\beta (\alpha_j - \beta)^T \mathrm X^T\mathrm X(\alpha_j - \beta) + \lambda \|\beta\|^2 + \lambda_{1,j}\|\beta\|_1 \end{aligned} \]

• 给定\(\mathrm B\)更新\(\mathrm A\)

子优化问题为 \[ \arg\min_{\mathrm A} \|\mathrm X - \mathrm X \mathrm B^T \mathrm A \|^2 \quad \text{s.t.} \mathrm A^T \mathrm A = \mathrm I_{k \times k} \] 利用Procrustes旋转的降秩表示结论，记SVD:\((\mathrm X^T \mathrm X) \mathrm B= \mathrm U\mathrm D \mathrm V^T\)，则解为 \[ \mathrm{\hat A} = \mathrm U \mathrm V^T \] note: 上面岭回归中\(\|\mathrm X - \mathrm X \mathrm {\hat B} \mathrm A^T\|^2 + \lambda \sum_{j=1}^k\|\beta_j\|^2\)化成了特征分解问题\(\text{tr}(\mathrm A^T\mathrm X^T \mathrm S_\lambda \mathrm X\mathrm A)\)，这是因为\(\hat\beta_j\)与\(\alpha_j\)有关（岭回归算子），但此处的\(\hat\beta_j\)是通过LARS-EN算法求解，与\(\alpha_j\)无直接关系，因此两个问题本质上有区别。

补充：Reduced Rank Procrustes Rotation

设\(M^T N\)的SVD:\(M^T N = U D V^T\)，则对约束优化问题 \[ \arg\min_{ A} \| M - N A^T\|^2 \quad \text{s.t.} A^T A = I_{k \times k} \] 下面对目标函数的范数展开，并利用正交约束和迹函数的性质可得 \[ \begin{aligned} &\| M - N A^T\|^2 \\ & = \text{tr}(M^T M) - 2\text{tr}(M^T NA^T) + \text{tr}(AN^TNA^T) \\ &\propto- 2\text{tr}(M^T NA^T) + \text{tr}(N^TNA^TA)\\ &\propto -2\text{tr}(M^T NA^T)\\ &= -2\text{tr}(UDV^TA^T)\\ &= -2\text{tr}(UD{A^*}^T)\\ &= -2\text{tr}({A^*}^T UD)\\ \end{aligned} \]

其中\(A^* = AV\)满足\({A^*}^T A^* = I\)，对角阵\(D\)由奇异值组成，因此优化问题寻找\({A^*}^T U\)对角元素为最大正数的条件。利用Cauchy-Schwartz不等式可知，当\(A^* = U\)时取最优解。因此\({\hat A} = U V^T\)。

算法流程

方差调整

传统PCA算法得到的主成分是无关的，载荷是相互正交的，但是稀疏化后无关性不在满足，这是因为\(\mathrm {\hat Z}^T \mathrm {\hat Z}\)不是严格的对角矩阵，为此需要对每个主成分做类似Schmidt 正交化，对每个主成分减去前面特征值方向的分量，从而保证正交性 \[ \mathrm {\hat Z}_{j\cdot 1,\ldots,j-1} = \mathrm {\hat Z}_{j} - \mathrm H_{1,\ldots,j-1} \mathrm {\hat Z}_{j} \] 其中\(\mathrm H_{1,\ldots,j-1}\)是投影矩阵，调整后主成分的方差为\(\sum_{j=1}^k \|\mathrm {\hat Z}_{j\cdot 1,\ldots,j-1}\|^2 = \text{tr} (\mathrm {\hat Z}^T \mathrm {\hat Z})\)（如果无关）。

少样本高纬度

上面的SPCA算法对\(p\gg n\)是适用的，不过计算量会很大，下面通过一刀切的方式进行简化，即令\(\lambda \to \infty\)。

令\(\mathrm {\hat V}_j (\lambda) = \frac{\hat \beta_j}{\|\hat \beta_j\|}\)， \[ \begin{aligned} (\mathrm{\hat A}, \mathrm{\hat B}) = &\arg\min_{\mathrm A,\mathrm B} -2\text{tr}(\mathrm A^T \mathrm X^T \mathrm X \mathrm B) + \sum_{j=1}^k\|\beta_j\|^2\\ & + \sum_{j=1}^k\lambda_{1,j}\|\beta_j\|_1 \quad \text{s.t.} \mathrm A^T \mathrm A = \mathrm I_{k \times k} \end{aligned} \] 当\(\lambda \to \infty\)有\(\mathrm {\hat V}_j (\lambda) \to \frac{\hat \beta_j}{\|\hat \beta_j\|}\)。

与SPCA算法相比，只有\(\mathrm{\hat B}\)的更新从Elastic Net问题变为如下稀疏优化问题 \[ \hat \beta_j = \arg\min_\beta -2\alpha_j^T (\mathrm X^T \mathrm X) \beta+\|\beta\|^2+\lambda_{1,j}\|\beta\|_1 \] 其解可通过软阈值算子(soft-thresholding)显示表达 \[ \hat \beta_j = (|\alpha_j^T \mathrm X^T \mathrm X|-\frac{\lambda_{1,j}}{2})_+ \text{sign} (\alpha_j^T \mathrm X^T \mathrm X) \]

半正定规划

参考A Mathematical Introduction to Data Science的4.4节

• 传统PCA可表示为

\[ \max_x x^T \Sigma x \quad \text{s.t.} \quad \|x\|_2 = 1 \]

由于 \[ x^T \Sigma x = \text{tr}(\Sigma (xx^T)) = \text{tr}(\Sigma X) \]

• 传统PCA等价表示

\[ \max_X \text{tr}(\Sigma X) \quad \text{s.t.} \quad \text{tr}( X) = 1, X \succeq 0 \]

该优化问题的最优解是第一个主成分矩阵，其秩为\(1\)。因此可以递归地对协方差阵\(\Sigma_k = \Sigma - \sum_{i<k} X_i\)使用该程序可得到前\(k\)个主成分。

• 稀疏PCA的半正定规划形式

\[ \max_X \text{tr}(\Sigma X) - \lambda \|X\|_1 \quad \text{s.t.} \quad \text{tr}( X) = 1, X \succeq 0 \]

其中\(\ell_1\)范数的凸化(convexification)可以保证主成分的稀疏性，即\(\#{X_{ij} \neq 0}\)非常小。

参考文献

1. Zou H, Hastie T, Tibshirani R, et al. Sparse Principal Component Analysis[J]. Journal of Computational and Graphical Statistics, 2006, 15(2): 265-286. ↩︎