写在前面

最近看了些结构化矩阵(如Hankel矩阵、Toeplitz矩阵)的低秩表示和近似问题，梳理下这篇文章^[1]。

结构保持降秩问题

给定任意矩阵\(A\in \mathbb R^{m\times n}\)，找到一个矩阵\(\hat B\in\Omega\)，其中\(\Omega\)表示一类特定的矩阵结构，在如下矩阵范数\(\|\cdot\|\)意义下求解一个秩\(k\in[1,\text{rank}(A)]\)近似问题 \[ \|A-\hat B\|=\min_{B}\|A-B\|,\text{s.t.}B\in\Omega,\text{rank}(B) = k \] 该结构化的低秩近似问题的解需要同时满足两个约束

• 由\(\Omega\)限制的结构
• 由\(k\)限制的秩

解的性质

在给出算法之前，一般都会去考虑解的存在性和唯一性等理论性质，下面就两个问题给出一些解释。

• 对可行集而言，结构化矩阵能否具有任意低的秩？
• 对于可解性而言，任意给定矩阵能否被一个具有特定结构和特定秩的矩阵近似？

只要可行集非空，如下近似问题必可解： \[ \min_{B}\|A-B\|,\text{s.t.}B\in\Omega,\text{rank}(B) \le k \] 其中\(\Omega\)是\(\mathbb R^{m\times n}\)的闭子集。该问题与原问题差在约束秩。\(\text{rank}(B) \le k\)的可行集为闭集可得\(\text{rank}(B) = k\)有解。但是反过来不一定成立。这是由于给定一个目标矩阵，可能不存在结构化的秩\(k\)近似，但是会存在结构化且秩低于\(k\)的近似。

下面给出两个特殊结构的结论

• 对称Toeplitz 矩阵可任意低秩近似(Symmetric Toeplitz matrices can have arbitrary lower rank.)
• \(n\times n\)的Hankel矩阵存在任意给定低秩矩阵近似(There are n × n Hankel matrices with any given lower rank.)

至于解的唯一性，若潜在矩阵维度是无穷大的，通过Hankel低秩矩阵，始终存在与Hankel矩阵的最接近的近似并且解是唯一的。然而，有限维情况下的结论尚未得到解决。

Lift-and-Project法

所有秩\(k\)矩阵构成一个曲面\(\mathscr R(k)\)，所有具有矩阵结构\(\Omega\)的空间构成另一个曲面，那么结构化的秩\(k\)矩阵可视为两个曲面的交集。Lift-and-Project法是一个线性收敛的方法来找到这个交空间的点。其核心思想是两个曲面上的交替投影来构造收敛的序列，序列的极限可同时满足两个约束，而收敛的过程中两个约束的距离越来越小。

算法步骤

设初始点\(A^{(0)} = A \in \Omega\)，迭代计数\(v=0,1,\ldots\)，交替迭代如下两个步骤直至收敛：

• Lift: 计算距离矩阵\(A^{(v)}\)最近的秩\(k\)矩阵\(B^{(v)} \in \mathscr R(k)\)；
• Project: 计算\(B^{(v)}\)到子空间\(\Omega\)的投影\(A^{(v+1)}\)；

几何解释

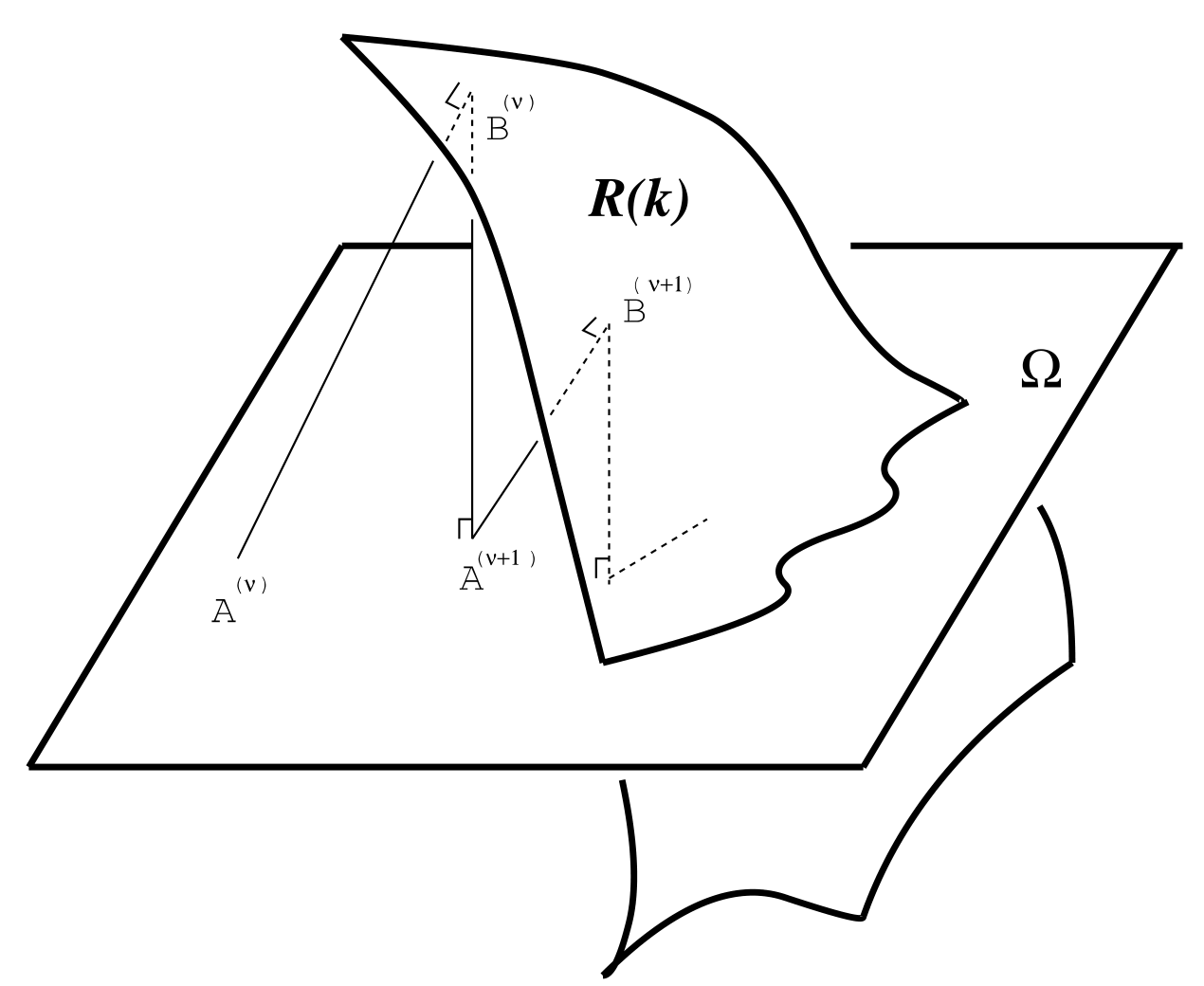
说明

• 第一步是一个矩阵的低秩近似问题，这个步骤与矩阵的结构无关，所以可以使用截断的奇异值分解算法来完成，用前\(k\)个奇异值和对应的奇异向量来重构出秩\(k\)矩阵。

• 第二步是矩阵的投影问题，这个解非常依赖于矩阵结构\(\Omega\)本身。对于简单的线性结构，解一般都是显示的闭解。例如Hankel矩阵和Toeplitz矩阵，仅需要做一个最小二乘取平均即得到投影矩阵。

• 算法得到两个序列\(\{A^{(v)}\}\)和\(\{B^{(v)}\}\)具有如下的下降性质： \[ \|A^{(v+1)}-B^{v+1}\|_F\le\|A^{(v+1)}-B^{v}\|_F\le\|A^{(v)}-B^{v}\|_F \] 因此，在Frobenius范数意义下，Lift-and-Project法是一个下降算法。

点对点的映射

如果上述Lift-and-Project法以\(T\in\Omega\)为初值迭代产生收敛的序列，定义映射 \[ P_k:\Omega\to\Omega \cap \mathscr R(k) \] 为该序列的极限点\(P_k(T)\)。

注意：

• 不要误解极限\(P_k(T)\)是\(\Omega\)中距离\(T\)最接近的秩\(k\)矩阵。
• 对任意矩阵\(A\)，\(P_k(A)\)不是结构保持降秩近似问题的解。

对称Toeplitz矩阵的分解式

秩为\(k\)的对称Toeplitz矩阵代数关系可分解为 \[ M(\alpha_1,\ldots,\alpha_k,\boldsymbol{y}^{(1)},\ldots,\boldsymbol{y}^{(1)}) = \sum_{i=1}^{k} \alpha_i \boldsymbol y^{(i)}{\boldsymbol y^{(i)}}^T =[m_{ij}] \] 其中向量\(y^{(i)}\)满足互正交关系 \[ \begin{aligned} &m_{j,j+s_1}=m_{1,s},\quad s=1,\ldots,n-1;j=2,\ldots,n-s+1\\ &\alpha_i \neq 0,{\boldsymbol y^{(i)}}^T\boldsymbol y^{(i)}=\delta_{ij},\quad i,j=1,\ldots,k. \end{aligned} \]

参考文献

1. Chu M T, Funderlic R E, Plemmons R J. Structured low rank approximation [J]. Linear algebra and its applications. 2003, 366: 157–172. ↩︎