写在前面

介绍一篇基于任务驱动下的字典学习^[1]，本文还参照了一个挺有意思的slide^[2]。

数据驱动字典学习

数据驱动字典学习强调的是数据自适应性，其目标是获取观测信号的字典实现最佳逼近的稀疏编码表示。假设训练集为\(\mathbf X=[\mathbf x_1,\ldots,\mathbf x_n]\)，经验损失函数为 \[ g_n (\mathbf D)\triangleq \frac{1}{n}\sum_{i=1}^n \ell_u (\mathbf x,\mathbf D) \] 其下标\(\ell_u\)表示无监督学习方式(unsupervised)。\(\ell_u (\mathbf x,\mathbf D)\)作为稀疏编码问题的最优值，可选用如下的elastic-net形式： \[ \ell_u (\mathbf x,\mathbf D) \triangleq \min_{\boldsymbol\alpha \in \mathbb R^p} \frac{1}{2}\|\mathbf x-\mathbf D\boldsymbol\alpha\|_2^2 + \lambda_1 \|\boldsymbol\alpha\|_1 + \frac{\lambda_2}{2}\|\boldsymbol\alpha\|_2^2 \]

• 当\(\lambda_2=0\)，\(\ell_u (\mathbf x,\mathbf D)\)导出\(\ell_1\)稀疏分解问题，见基追踪(basis pursuit)、Lasso等相关论文。

• 为避免字典原子出现\(\ell_2\)范式任意大的问题，通常限制字典如下约束 \[ \mathcal D \triangleq \{\mathbf D \in \mathbb R^{m \times p} \text{s.t.} \forall j \in \{1,\ldots,p\},\|\mathbf d_j\|_2 \leq 1 \} \]

• 经验损失到期望损失： \[ \mathbb E_{\mathbf x}[\ell_u (\mathbf x,\mathbf D)] \stackrel{\text{a.s.}}{=}\lim_{n \to \infty} g_n(\mathbf D) \]

稀疏表示

稀疏表示是采用基函数对原始数据进行编码，可以简单地理解为线性表示。

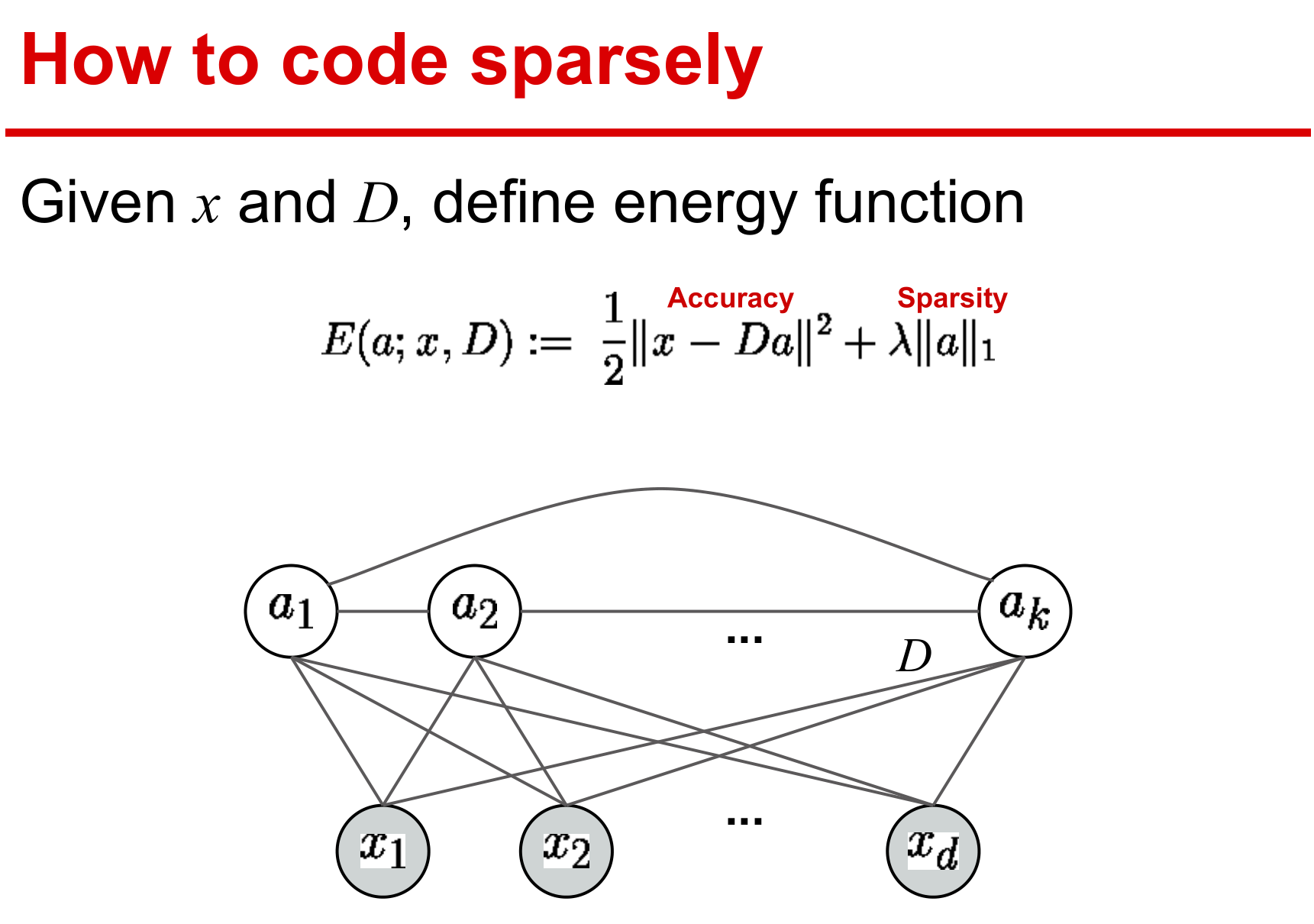
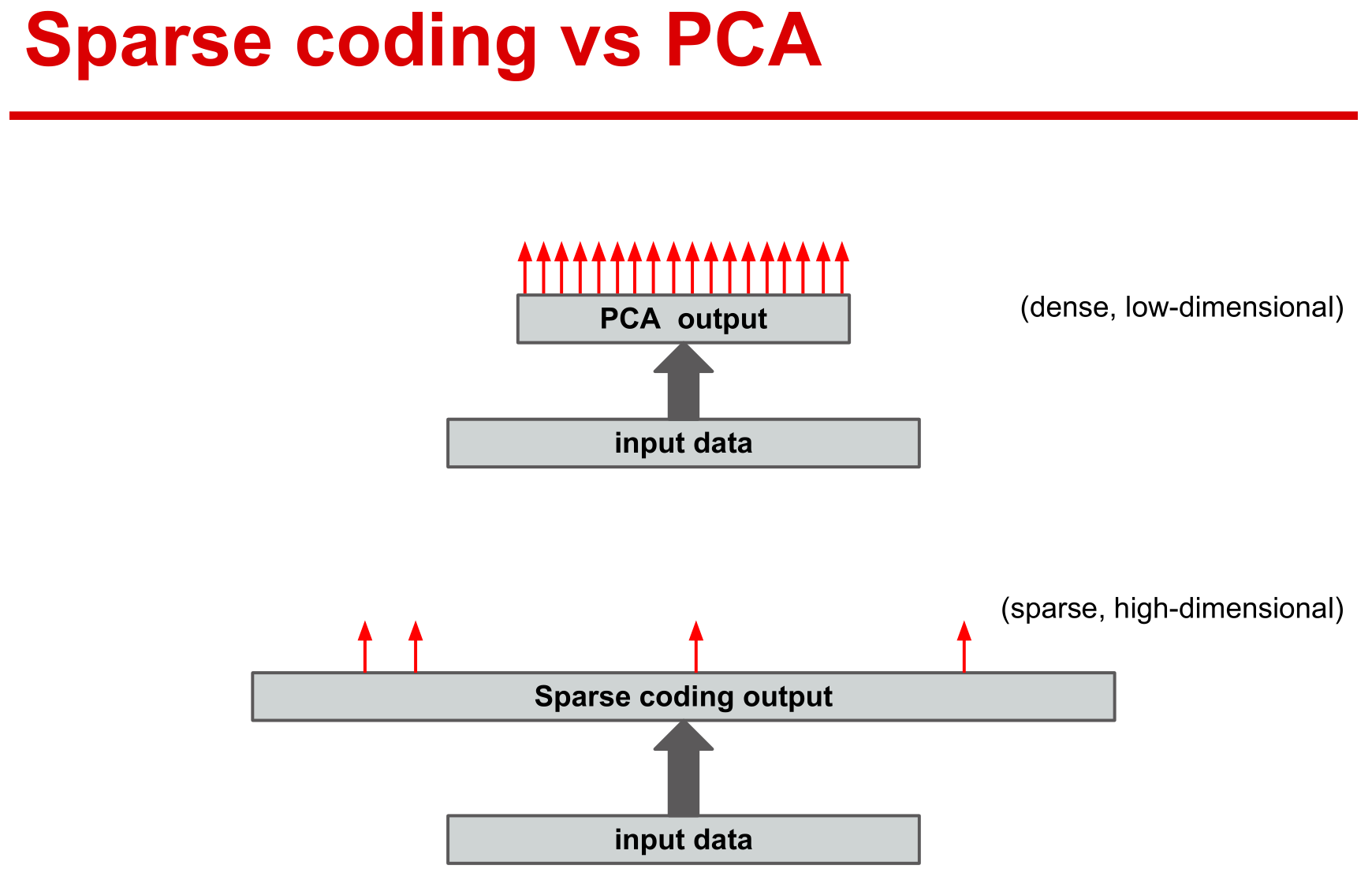
稀疏表示则采用冗余的基函数，而主成分分析采用正交基来重构数据，所以主成分分析的系数并非稀疏。

字典学习

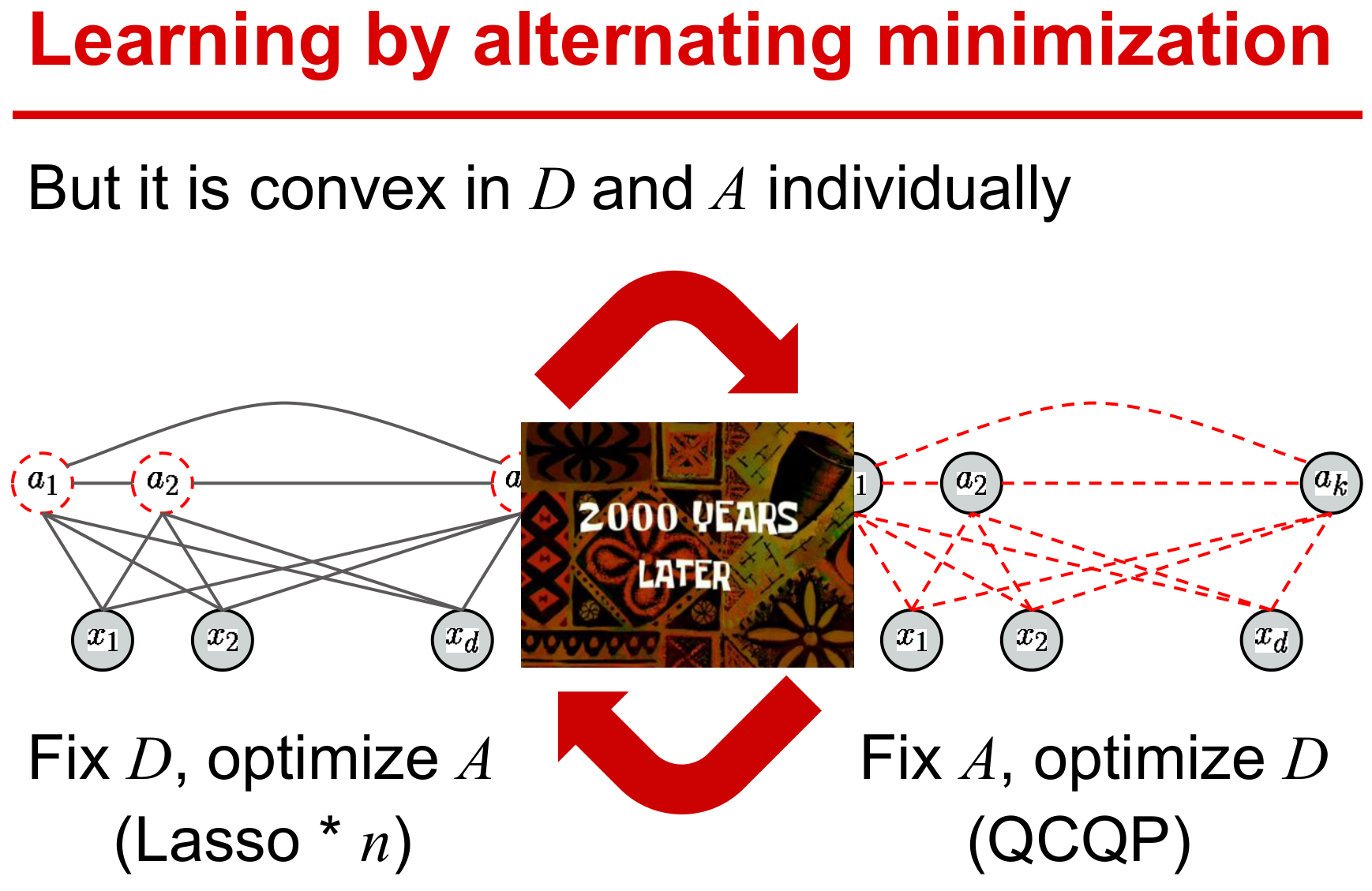
字典学习需要同时求解字典和稀疏编码，优化对两个变量而言是非凸的。

但是对单个变量是凸的，所以采用交替迭代的方式进行变量更新。

监督学习方式

基本形式

记elastic-net的稀疏解为 \[ \boldsymbol\alpha^\star(\mathbf x,\mathbf D)\triangleq \operatorname*{arg\,min}_{\boldsymbol\alpha \in \mathbb R^p} \frac{1}{2}\|\mathbf x-\mathbf D\boldsymbol\alpha\|_2^2 + \lambda_1 \|\boldsymbol\alpha\|_1 + \frac{\lambda_2}{2}\|\boldsymbol\alpha\|_2^2 \] 下面使用稀疏向量\(\boldsymbol\alpha^\star(\mathbf x,\mathbf D)\)作为信号\(\mathbf x\)的特征来估计对应的标签\(\mathbf y\)，一般都是最小化期望风险 \[ \min_{\mathbf W\in\mathcal W} f(\mathbf W) + \frac{\nu}{2}\|\mathbf W\|_F^2 \] 其中\(\mathbf W\)是需要学习的模型参数。凸函数\(f\)定义如下： \[ f(\mathbf W) \triangleq \mathbb E_{\mathbf y,\mathbf x}[\ell_s (\mathbf y,\mathbf W,\boldsymbol\alpha^\star(\mathbf x,\mathbf D))] \] 与\(\ell_u\)不同，在给定模型参数\(\mathbf W\)和\(\boldsymbol\alpha^\star(\mathbf x,\mathbf D)\)稀疏特征下，\(\ell_s\)度量了预测标签与真实标签的接近程度，所以\(\ell_s\)是以监督学习(supervised)的方式选择不同的损失函数，例如二次函数、logistic函数或hinge函数等。注意，到目前为止，所用的字典都是无监督学习\(\ell_u (\mathbf x,\mathbf D)\)最优化得到的，但用来重构的字典\(\mathbf D\)并不适用于监督学习任务，这就有了如下监督学习的方式 \[ \min_{\mathbf D\in\mathcal D,\mathbf W\in\mathcal W} f(\mathbf D,\mathbf W) + \frac{\nu}{2}\|\mathbf W\|_F^2 \] 其中\(f(\mathbf D,\mathbf W)\)则需要同时学习参数\(\mathbf W\)和字典\(\mathbf D\)。 \[ f(\mathbf D,\mathbf W) \triangleq \mathbb E_{\mathbf y,\mathbf x}[\ell_s (\mathbf y,\mathbf W,\boldsymbol\alpha^\star(\mathbf x,\mathbf D))] \]

• 引入字典变量\(\mathbf D\)后，\(\boldsymbol\alpha^\star\)的不可微分不利于优化问题的求解。
• 常规做法是引入稀疏正则化的光滑近似项。

监督与非监督的区别在于字典的过完备性：

• 非监督是衡量预测样本与真实样本的误差，需要冗余的稀疏表示
• 监督则衡量预测标签与真实标签的差异，仅需要获取具有鉴别的特征，严格的过完备不再需要。

传统的监督学习先获取数据表示，再挖掘特征，这是一种典型的多步骤式的机器学习方式，每一步最优的并不代表整体工程最优。

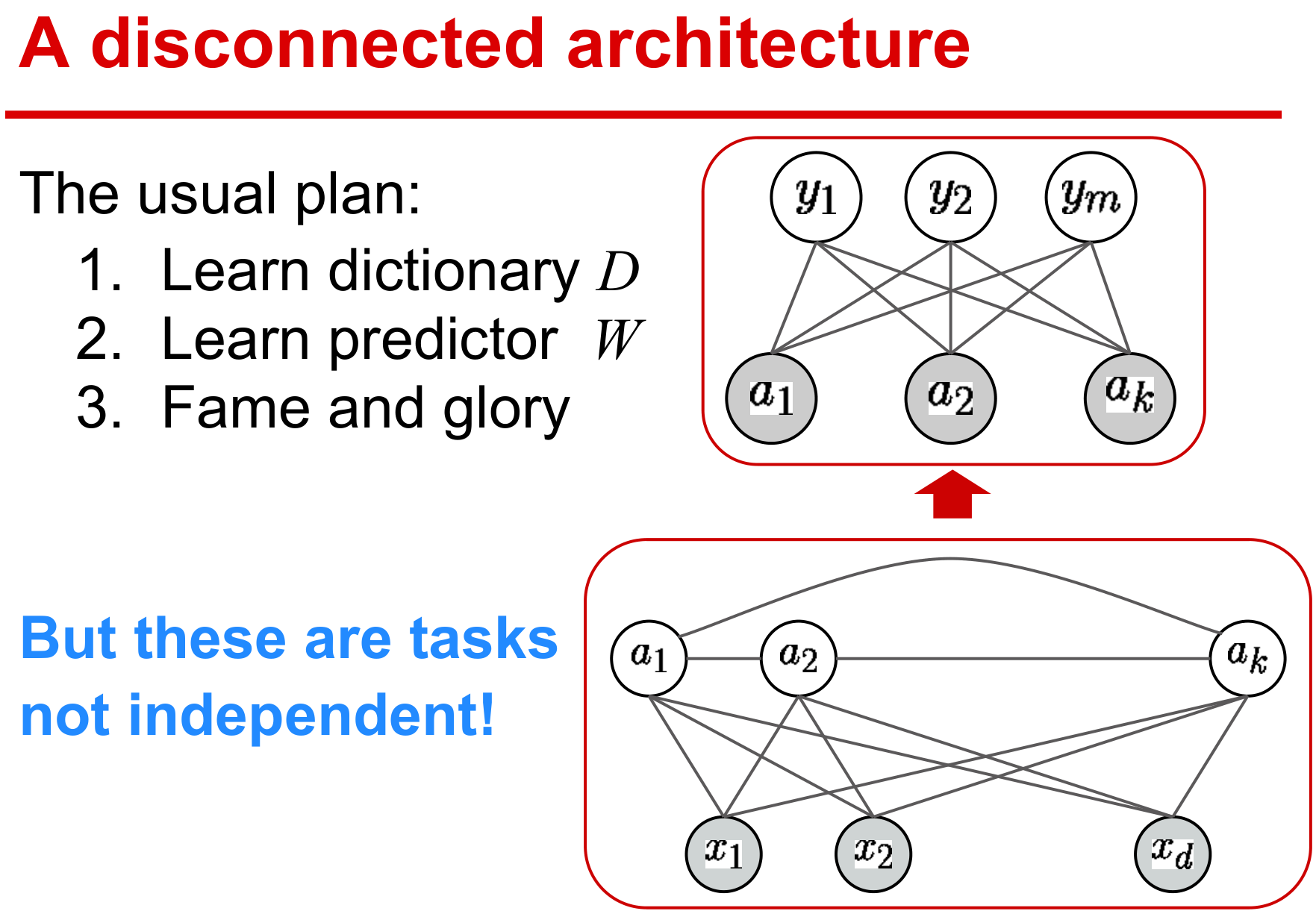
目前方法都期望设计端到端的学习方式，在统一的结构下学习有效参数，保证整体性能最优。

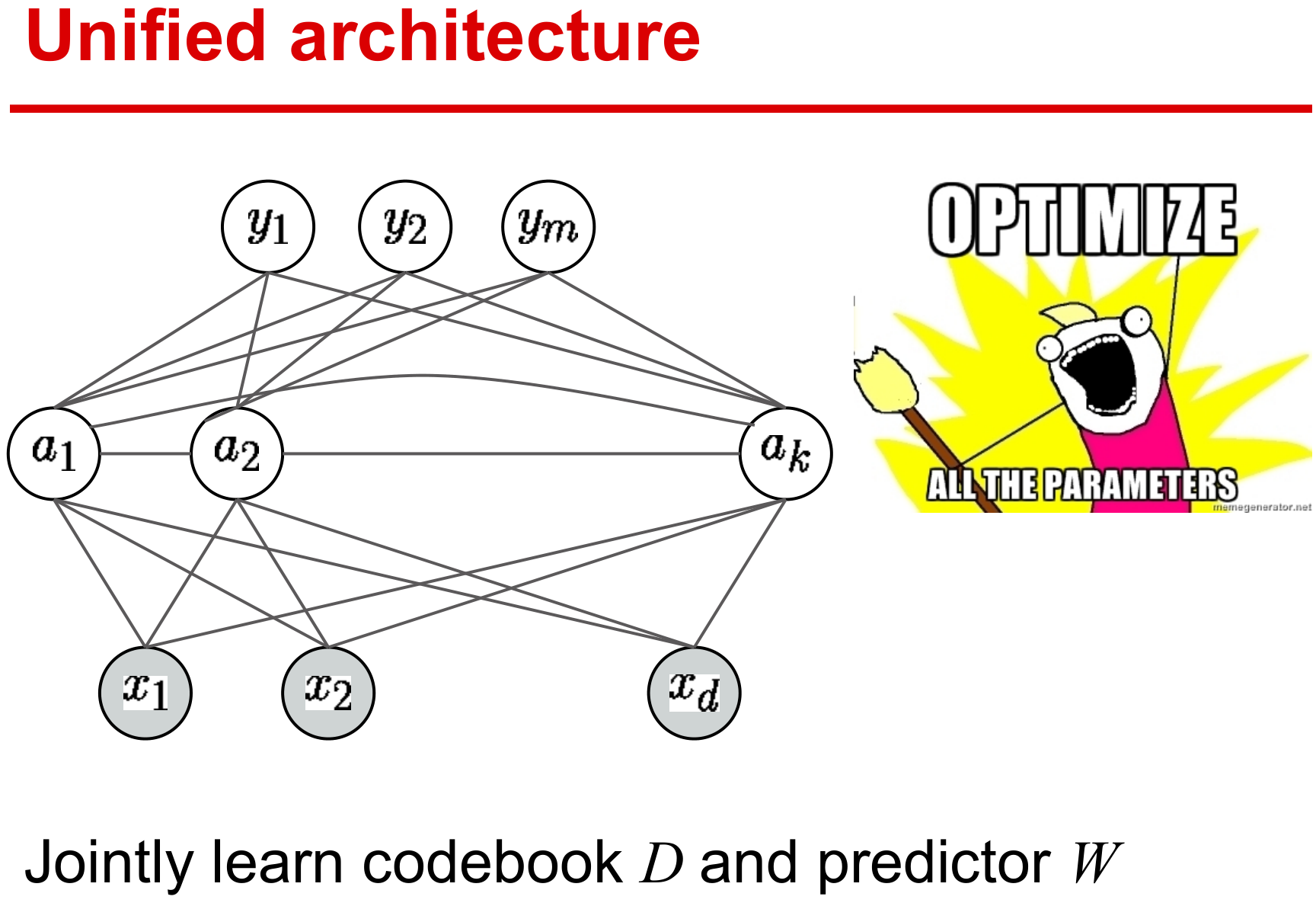
基本假设

• \((\mathbf y,\mathbf x)\)服从概率密度函数\(p\)，其紧支撑集\(K_{\mathcal Y} \times K_{\mathcal X} \subseteq \mathcal Y \times \mathcal X\)。
• 当\(\mathcal Y\)为有限维实向量空间的子集时，\(p\)为连续且\(\ell_s\)二次连续可微。
• 当\(\mathcal Y\)为有限的标签集合时，\(p(\mathbf y,\cdot)\)为连续且\(\ell_s(\mathbf y,\cdot)\)二次连续可微。

输入数据的线性变换

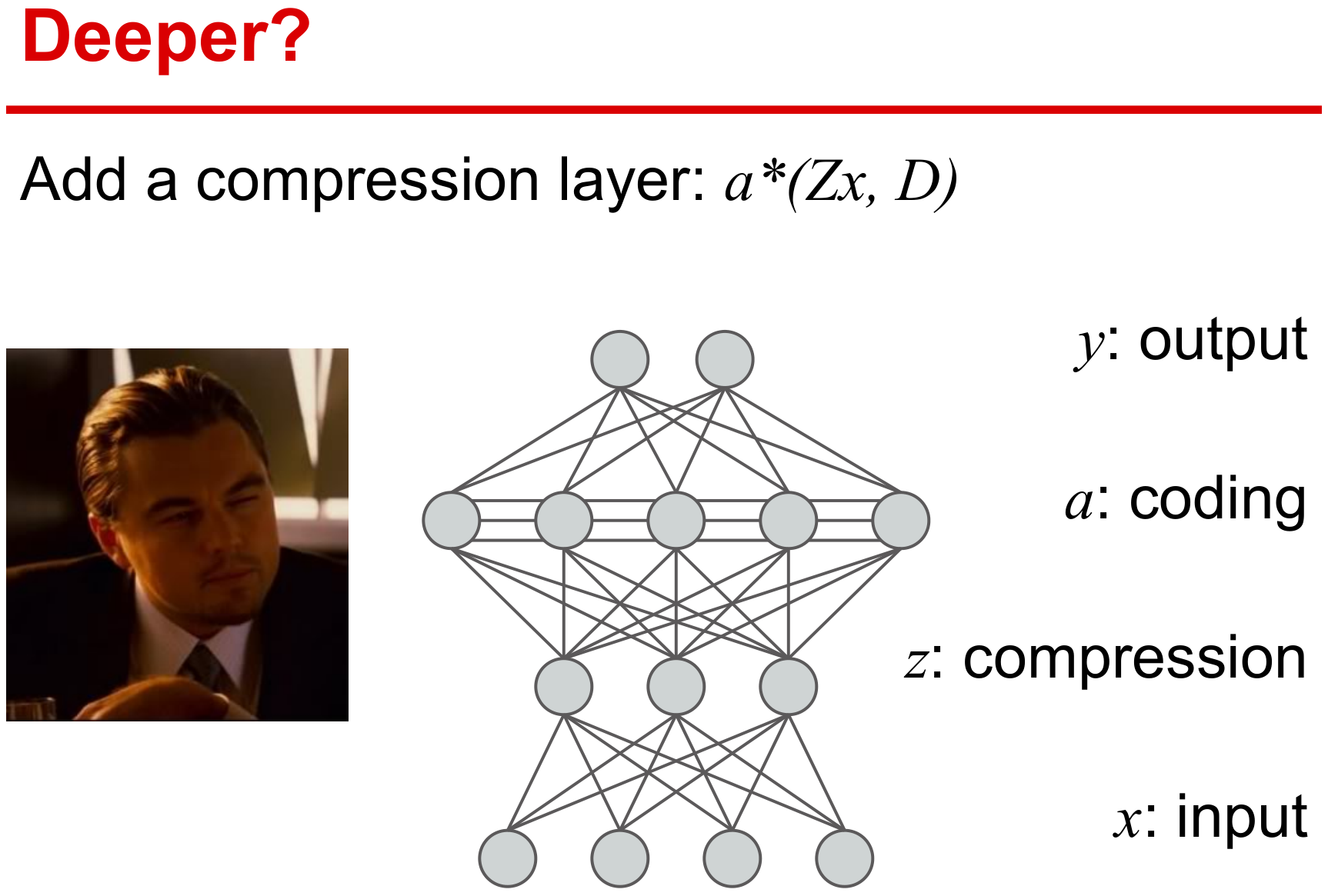
在监督学习基本形式上，考虑增加一个线性变换\(\mathbf Z\)得到如下模型 \[ \min_{\mathbf D \in \mathcal D, \mathbf W \in \mathcal W, \mathbf Z \in \mathcal Z} f(\mathbf D,\mathbf W,\mathbf Z) +\frac{\nu_1}{2}\|\mathbf W\|_F^2 + \frac{\nu_2}{2}\|\mathbf Z\|_F^2 \] 其中\(f(\mathbf D,\mathbf W,\mathbf Z)\)则需要同时学习参数\(\mathbf W\)、字典\(\mathbf D\)和线性变换\(\mathbf Z\)。 \[ f(\mathbf D,\mathbf W,\mathbf Z) \triangleq \mathbb E_{\mathbf y,\mathbf x}[\ell_s (\mathbf y,\mathbf W,\boldsymbol\alpha^\star(\mathbf Z\mathbf x,\mathbf D))] \] 该线性变换\(\mathbf Z\)具有如下作用：

• 通过线性变换可降低特征空间的维度
• 通过增加模型的参数使得模型表现能力更强

半监督学习

稀疏编码技术可有效地从无标签数据中学习到好的特征，因此下面给出一个监督和无监督相结合的半监督模型。 \[ \min_{\mathbf D \in \mathcal D, \mathbf W \in \mathcal W} (1-\mu)\mathbb E_{\mathbf y,\mathbf x} [\ell_s\big(\mathbf y,\mathbf W, \boldsymbol\alpha^\star (\mathbf x,\mathbf D)\big)] + \mu \mathbb E_{\mathbf x} [\ell_u(\mathbf x,\mathbf D)] + \frac{\nu}{2}\|\mathbf W\|_F^2 \]

任务驱动字典学习

下面将前面的基本优化模型应用至多种任务上，例如回归、分类、压缩感知。分类可视为回归的特殊形式，即在向量空间中选择有限的离散数据作为标签。大多分类算法也都是集中研究二分类算法，多分类可通过多个二分类器组合实现。注意，下面介绍的应用中，\(\ell_s\)的只需要满足前面提到的二次可微即可。

回归

在回归任务中，目标函数的\(\ell_s\)通常选择为平方损失函数，这在贝叶斯估计中也可解释去除高斯噪声的残差项，因此回归也可视为一种去噪或恢复的过程。

\[ \min_{\mathbf D \in \mathcal D, \mathbf W \in \mathcal W} \mathbb E_{\mathbf y,\mathbf x} \Big[\frac{1}{2}\|\mathbf y-\mathbf W \boldsymbol\alpha^\star (\mathbf x,\mathbf D)\|_2^2\Big]+\frac{\nu}{2}\|\mathbf W\|_F^2 \]

当然，\(\ell_s\)也可使用其他的二次可微损失函数来衡量\(\mathbf y\)与\(\mathbf W \boldsymbol\alpha^\star (\mathbf x,\mathbf D)\)的差异性。

二分类

设置标签集为\(\mathcal Y=\{-1; +1\}\)，\(\ell_s\)使用logistic回归损失函数来表示标签\(y\)与特征\(\boldsymbol\alpha^\star(\mathbf x,\mathbf D)\)之间的关系。对应的线性模型如下：

\[ \min_{\mathbf w \in \mathbb R^p,\mathbf D \in \mathcal D} \mathbb E_{y,\mathbf x} \Big[\log\big(1+e^{-y \mathbf w^\top \boldsymbol\alpha^\star(\mathbf x,\mathbf D)}\big)\Big]+\frac{\nu}{2}\|\mathbf w\|_2^2 \]

求解得到最优解\((\mathbf w,\mathbf D)\)后，对新的样本\(\mathbf x\)，计算\(\text{sgn}(\mathbf w^\top \boldsymbol\alpha^\star(\mathbf x,\mathbf D))\)作为预测的类别。此外还有一种双线性的矩阵变体模型，利用\(\mathbf x^\top \mathbf W \boldsymbol\alpha^\star(\mathbf x,\mathbf D)\)来判断类别标签。

\[ \min_{\mathbf w \in \mathbb R^{m \times p},\mathbf D \in \mathcal D} \mathbb E_{y,\mathbf x}\Big[\log\big(1+e^{-y \mathbf x^\top \mathbf W \boldsymbol\alpha^\star(\mathbf x,\mathbf D)}\big)\Big] + \frac{\nu}{2}\|\mathbf W\|_F^2 \]

线性模型(向量形式)需要学习\(p\)个参数，而双线性模型(矩阵形式)需要学习\(pm\)个参数，因此双线性模型能学习到的特征比线性更丰富，但也可能出现过拟合的问题。

优化

与非监督字典学习方式一样，总的优化问题对所有变量而言非凸，但对每个变量是凸的，因此优化算法一般采用交替迭代方式。这便需要将原问题划分为多个可解的子问题，然后计算各自的梯度即可。

函数求导

满足三个基本假设下，函数\(f(\mathbf D,\mathbf W) \triangleq \mathbb E_{\mathbf y,\mathbf x}[\ell_s (\mathbf y,\mathbf W,\boldsymbol\alpha^\star(\mathbf x,\mathbf D))]\)是可微的，其导数为 \[ \left\{ \begin{aligned} \nabla_\mathbf W f(\mathbf D,\mathbf W) & = \mathbb E_{\mathbf y,\mathbf x}[\nabla_\mathbf W \ell_s(\mathbf y,\mathbf W,\boldsymbol\alpha^\star)], \\ \nabla_\mathbf D f(\mathbf D,\mathbf W) & = \mathbb E_{\mathbf y,\mathbf x}[-\mathbf D\boldsymbol\beta^\star\boldsymbol\alpha^{\star\top} + (\mathbf x-\mathbf D\boldsymbol\alpha^\star) \boldsymbol\beta^{\star\top}], \\ \end{aligned} \right. \] 记\(\Lambda\)为稀疏编码\(\boldsymbol\alpha^\star(\mathbf x,\mathbf D)\)的非零系数指标集，上式中向量\(\boldsymbol\beta^{\star}\)的最优条件为 \[ \left \{\begin{aligned} &\boldsymbol\beta^\star_{\Lambda^C} = 0 \\ &\boldsymbol\beta^\star_{\Lambda} = (\mathbf D_\Lambda^\top \mathbf D_\Lambda+\lambda_2 \mathbf I)^{-1} \nabla_{\boldsymbol\alpha_\Lambda} \ell_s(\mathbf y,\mathbf W,\boldsymbol\alpha^\star)\\ \end{aligned} \right. \] 满足三个基本假设下，函数\(f(\mathbf D,\mathbf W,\mathbf Z) \triangleq \mathbb E_{\mathbf y,\mathbf x}[\ell_s (\mathbf y,\mathbf W,\boldsymbol\alpha^\star(\mathbf Z\mathbf x,\mathbf D))]\)是可微的，其导数为 \[ \left\{ \begin{aligned} \nabla_\mathbf W f(\mathbf D,\mathbf W) & = \mathbb E_{\mathbf y,\mathbf x}[\nabla_\mathbf W \ell_s(\mathbf y,\mathbf W,\boldsymbol\alpha^\star)], \\ \nabla_\mathbf D f(\mathbf D,\mathbf W) & = \mathbb E_{\mathbf y,\mathbf x}[-\mathbf D\boldsymbol\beta^\star\boldsymbol\alpha^{\star\top} + (\mathbf Z\mathbf x-\mathbf D\boldsymbol\alpha^\star) \boldsymbol\beta^{\star\top}], \\ \nabla_\mathbf Z f(\mathbf D,\mathbf W) & = \mathbb E_{\mathbf y,\mathbf x}[\mathbf D\boldsymbol\beta^\star\mathbf x^\top], \\ \end{aligned} \right. \]

算法

随机梯度下降算法是一类典型应对含有期望项的目标函数。下面给一个投影一阶随机梯度下降算法流程。

说明：

• step 3中采用一种典型的同伦法LARS算法来解决elastic-net稀疏优化问题
• 矩阵\((\mathbf D_\Lambda^\top \mathbf D_\Lambda+\lambda_2\mathbf I)^{-1}\)具有Cholesky分解形式，可快速计算\(\boldsymbol\beta^\star\)
• 学习率\(\rho_t\)采用启发式方式选择：\(\min(\rho,\rho t_0/t)\)
  • 当\(t < t_0\)，使用常数学习率\(\rho\)
  • 当\(t > t_0\)，学习率每次递减\(1/t\)
• 采用小批量策略(\(\eta > 1\))提高算法的收敛速度
• 字典的初值可选用无监督学习获得，可使用SPAMS工具箱。

两个推广模型的修改

前面有输入数据的线性变换和半监督学习的两个改进版本，算法部分只需要修改其中对应步骤。

• 输入数据的线性变换关于\(\mathbf Z\)的梯度

\[ \mathbf Z \leftarrow \Pi_{\mathcal Z}\Big[\mathbf Z - \rho_t (\mathbf D\boldsymbol\beta^\star\mathbf x^{\top}+\nu_2\mathbf Z)\Big], \]

• 半监督学习关于\(\mathbf D\)的梯度

\[ \begin{aligned} \mathbf D \leftarrow \Pi_{\mathcal D}\Big[\mathbf D - \rho_t \Big( &(1-\mu) \big(-\mathbf D \boldsymbol\beta^\star \boldsymbol\alpha^{\star\top} + (\mathbf x_t-\mathbf D \boldsymbol\alpha^\star)\boldsymbol\beta^{\star\top}\big) \\ &+ \mu\big(-(\mathbf x^\prime_t-\mathbf D \boldsymbol\alpha^{\star\prime})\boldsymbol\alpha^{\star\prime\top}\big) \Big) \Big] \end{aligned} \]

小结

本文给出一个任务驱动字典学习的框架，给出一个通用的求解算法，并从理论上给出优化最优性条件（见附录）。文章虽然是12年的文章，但是目前在其他邻域没有见到类似的任务驱动学习范式，另外最近张量表示比较火，可是做下张量形式的任务驱动字典学习。

另外slide^[2]里给了一个深度的展望，这个目前有一些卷积稀疏编码网络的工作（见Elad组^[3]），后面如果有精力可以再写写这些方面的文章。

References

1. J. Mairal, F. Bach and J. Ponce.Task-Driven Dictionary Learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 34, no. 4, pp. 791-804, 2012, doi: 10.1109/TPAMI.2011.156. ↩︎
2. Slide: http://cseweb.ucsd.edu/~dasgupta/254-deep/brian.pdf ↩︎
3. Michael Elad Homepage: https://elad.cs.technion.ac.il ↩︎