介绍变分非线性线性调频模态分解(variational nonlinear chirp mode decomposition, VNCMD)^[1]

写在前面

变分模态分析(VMD)算法是基于窄带(narrow-band)信号设计的，不适于宽带(wide-band)信号。作为宽带信号一个典型例子，非线性调频信号(nonlinear chirp signals, NCSs)的时变频率特性导致传统算法仅能获取全局频率信息。而多个非线性调频模态的叠加对信号的分析更具挑战性。非线性调频信号性质与VMD模型的结合产生了非线性线性调频模态分解(VNCMD)。

VNCMD模型

\[ \begin{aligned} &\min_{u_i(t),v_i(t),{\hat f}_i(t)} \sum_{i=1}^Q \left(\|u_i^{\prime\prime} (t)\|_2^2 + \|v_i^{\prime\prime} (t)\|_2^2 \right) \\ &\text{s.t.} \|g(t) - \sum_{i=1}^Q u_i(t)\cos(2\pi \int_0^t \hat f_i(s) ds) + v_i(t)\sin(2\pi \int_0^t \hat f_i(s) ds)\|_2 \leq \varepsilon \end{aligned} \]

非线性调频模态

非线性调频模态(nonlinear chirp mode)用基本的调幅调频(AM-FM)信号来刻画 \[ g(t) = a(t)\cos(2\pi \int_0^t f(s)ds + \phi) \]

解析信号

模态运用Hilbert变换可得 \[ \begin{aligned} g_A (t) &= g(t) + j{\mathcal H}(g(t)) \\ &\approx a(t)\exp(j(2\pi \int_0^t f(s)ds + \phi)) \end{aligned} \]

算子

记\(f_d(s)\)为频率函数，\(f_c >0\)为载频

• 解调算子(demodulation operator, DO)

\[ \Phi ^- (t) = \exp (-j2\pi (\int_o^tf_d(s)ds - f_c t)) \]

• 调制算子(modulation operator, MO)

\[ \Phi ^+ (t) = \exp (j2\pi (\int_o^tf_d(s)ds - f_c t)) \]

显然，解调算子与调制算子互逆 \[ \Phi ^- (t) \cdot \Phi ^+ (t) = 1 \] 算子对解析信号作用后得到 \[ \begin{aligned} g_A^d(t) &= g_A(t) \Phi ^- (t) \\ &= a(t)\exp(j(2\pi f_c t + 2\pi \int_0^t (f(s) - f_d(s))ds + \phi))\\ g(t) &=g_A^d(t) \Phi ^+ (t) \\ &= a(t)\exp(j(2\pi \int_0^t f(s)ds + \phi)) \end{aligned} \] 实际上，算子也可直接应用至实信号上 \[ \begin{aligned} \Re(g_{A}^{d})&=\Re(g_{A}) \cdot \Re(\Phi^{-}) -\Im (g_{A}) \cdot Im(\Phi^{-}) \\ \Re(g_{A})&=\Re(g_{A}^{d}) \cdot \Re(\Phi^{+}) -\Im (g_{A}^{d}) \cdot Im(\Phi^{+}) \end{aligned} \]

调制流程

通过解调技术讲宽带信号转化为窄带信号。在最理想的情况下\(f_d(s) = f(s)\)，解调信号\(g_A^d(t)\)是一个纯调幅(AM)信号，意味着具有最窄的带宽。不仅可估计频率信息，而且能重构非线性调频模态。

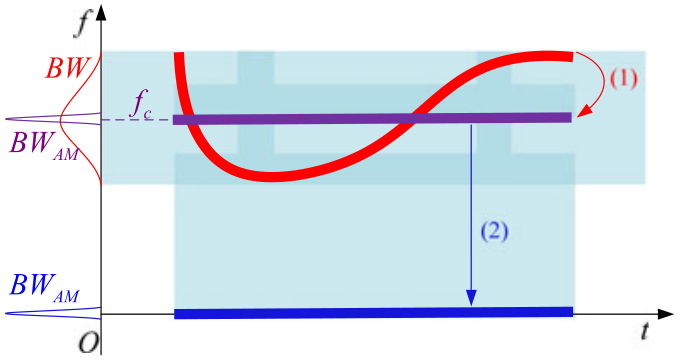
• 用解调算子估计NCM的FM项

\[ g_A^d(t) = g_A(t) \exp (-j2\pi (\int_o^tf_d(s)ds - f_c t)) \]

• 将解调信号移至基带信号来估计带宽

\[ g_A^b(t) = g_A^d(t) \exp (-j2\pi f_c t) \]

这两步可一步完成 \[ g_A^b(t) = g_A(t)\exp (-j2\pi\int_o^tf_d(s)ds) \] 频率平移的目的是用最大的频率估计带宽。VMD仅实现了频率平移，所以对非线性调频信号，既不能提取瞬时频率也不能改变带宽。

非线性调频信号

非线性调频信号(nonlinear chirp signal)是多种非线性调频模态叠加并收到噪声干扰观察得到 \[ \begin{aligned} g(t) = \sum_i ^Q & a_i(t)\cos(2\pi \int_0^t f_i(s)ds + \phi_i) + n(t)\\ = \sum_i ^Q & u_i(t)\cos(2\pi \int_0^t \hat f_i(s)ds) \\ &+ v_i(t)\sin(2\pi \int_0^t \hat f_i(s)ds) + n(t) \end{aligned} \] 其中解调信号\(u_i(t),v_i(t)\)表示如下 \[ \begin{aligned} u_i &= a_i(t)\cos(2\pi \int_0^t (f_i(s) - \hat f_i(s))ds + \phi_i)\\ u_i &= -a_i(t)\sin(2\pi \int_0^t (f_i(s) - \hat f_i(s))ds + \phi_i) \end{aligned} \] 其中\(\hat f_i\)的作用是解调至窄带并频率移动，即DO算子的频率函数。这种实虚部表示直接应用至VNCMD模型的约束条件上。

有了这些基础，我们回到模型的目标函数上 \[ \min_{u_i(t),v_i(t),\hat f_i(t)} \sum_{i=1}^Q \left(\|u_i^{\prime\prime} (t)\|_2^2 + \|v_i^{\prime\prime} (t)\|_2^2\right) \]

• \(u_i,v_i\)是刻画NCM的实部和虚部经过解调算子后的结果
• 二阶导的\(\ell _2\)范数可度量解调信号的带宽
• 寻找最优的\(\hat f_i\)可以将AM-FM信号转为AM信号
• 非线性调频信号假设\(\hat f_i\)为光滑且缓慢变化的函数
• 当\(\hat f_i\)设置为常数时，VNCMD模型等价于VMD模型

模型离散化

\[ \begin{aligned} &\min_{\mathbf u_i, \mathbf v_i, \mathbf f_i} \sum_{i} \left(\|\Omega\mathbf u_i \|_2^2 + \|\Omega\mathbf v_i \|_2^2\right)\\ &\text{s.t.} \left\|\mathbf g - \sum_{i} \left(\mathbf A_i \mathbf u_i + \mathbf B_i \mathbf v_i\right)\right\|_2 \leq \varepsilon \end{aligned} \]

其中向量都是按采样时间离散化 \[ \begin{aligned} \mathbf u_i &= [u_i(t_0), \dots, u_i(t_{N-1})]^T\\ \mathbf v_i &= [v_i(t_0), \dots, v_i(t_{N-1})]^T\\ \mathbf f_i &= [\hat f_i(t_0), \dots, \hat f_i(t_{N-1})]^T\\ \mathbf g &= [g_i(t_0), \dots, g_i(t_{N-1})]^T\\ \mathbf A_i &= \operatorname{diag}[\cos \varphi_i(t_0), \dots, \cos \varphi_i(t_{N-1})]\\ \mathbf B_i &= \operatorname{diag}[\sin \varphi_i(t_0), \dots, \sin \varphi_i(t_{N-1})]\\ \varphi_i(t) &=2\pi \int_0^t \hat f_i(s)ds \end{aligned} \] 微分算子\((\cdot ^{\prime\prime})\)被矩阵\(\Omega\)代替 \[ \Omega = \left[\begin{matrix} -1 & 1 & 0 & \cdots & 0 \\ 1 & -2 & 1 & \cdots & 0 \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & \cdots & 1 & -2 & 1 \\ 0 & \cdots & 0 & 1 & -1 \end{matrix}\right] \] 约束条件\(\left\|\mathbf g - \sum_{i} \left(\mathbf A_i \mathbf u_i + \mathbf B_i \mathbf v_i\right)\right\|_2 \leq \varepsilon\)可用欧式球\(\mathcal C_\varepsilon = \{ \|c\|_2 \leq \varepsilon\}\) 和示性函数\(\mathcal I_{\mathcal C_\varepsilon}(z) = \begin{cases} 0, & z\in \mathcal C_\varepsilon \\ +\infty, & z\notin\mathcal C_\varepsilon \end{cases}\)转换，引入噪声成分\(\mathbf w\) \[ \begin{aligned} &\min_{\mathbf u_i, \mathbf v_i, \mathbf f_i, \mathbf w} \mathcal I_{\mathcal C_\varepsilon}(\mathbf w) + \sum_{i} \left(\|\Omega\mathbf u_i \|_2^2 + \|\Omega\mathbf v_i \|_2^2\right)\\ &\text{s.t.} \quad \mathbf w = \mathbf g - \sum_{i} \left(\mathbf A_i \mathbf u_i + \mathbf B_i \mathbf v_i\right) \end{aligned} \] 化约束条件为无约束优化问题，构造如下增广的Lagrangian函数 \[ \begin{aligned} \mathcal{L} ( \mathbf u_i, \mathbf v_i, \mathbf f_i, \mathbf w, \lambda ) &= \mathcal I_{\mathcal C_\varepsilon}(\mathbf w) + \sum_{i} \left(\|\Omega\mathbf u_i \|_2^2 + \|\Omega\mathbf v_i \|_2^2\right)\\ &+\frac{\alpha}{2}\Bigg\Vert \mathbf w - \mathbf g + \sum_{i} \left(\mathbf A_i \mathbf u_i + \mathbf B_i \mathbf v_i\right)\Bigg\Vert_2^2\\ &+ \Bigg\langle\lambda,\mathbf w - \mathbf g + \sum_{i} \left(\mathbf A_i \mathbf u_i + \mathbf B_i \mathbf v_i\right)\Bigg\rangle\\ &= \mathcal I_{\mathcal C_\varepsilon}(\mathbf w) + \sum_{i} \left(\|\Omega\mathbf u_i \|_2^2 + \|\Omega\mathbf v_i \|_2^2\right)\\ &+\frac{\alpha}{2}\Bigg\Vert \mathbf w - \mathbf g + \sum_{i} \left(\mathbf A_i \mathbf u_i + \mathbf B_i \mathbf v_i\right) + \frac{\lambda}{\alpha}\Bigg\Vert_2^2 - \frac{\|\lambda\|_2^2}{2\alpha} \end{aligned} \] 该模型可通过ADMM算法分解为若干个子问题，并交替更新各个变量

• 更新\(w\)

\[ \arg\min_w \mathcal I_{\mathcal C_\varepsilon}(\mathbf w) + \frac{\alpha}{2}\Bigg\Vert \mathbf w - \mathbf g + \sum_{i} \left(\mathbf A_i \mathbf u_i + \mathbf B_i \mathbf v_i\right) + \frac{\lambda}{\alpha}\Bigg\Vert_2^2 \]

该子问题可抽象为如下优化问题，可通过近邻算子(proximity operator)求解 \[ \operatorname{prox}_{\mathcal C_\varepsilon / \alpha}(x) = \arg\min_w \mathcal I_{\mathcal C_\varepsilon}(w) + \frac{\alpha}{2} \|w-x\|_2^2 \] 凸集\(\mathcal C_\varepsilon\)示性函数的近邻算子\(\operatorname{prox}_{\mathcal C_\varepsilon / \alpha}(x)\)等价于\(\mathcal C_\varepsilon\)上的投影 \[ \operatorname{prox}_{\mathcal C_\varepsilon / \alpha}(x) = \mathcal P _{\mathcal C_\varepsilon} (x) = \begin{cases} \frac{\varepsilon x}{\|x\|_2}, & \|x\|_2 > \varepsilon \\ x, & \|x\|_2 \leq \varepsilon \end{cases} \] 因此该子问题的解可显性表达 \[ \mathbf w^{k+1} = \mathcal P _{\mathcal C_\varepsilon} (\mathbf g - \sum_{i} \left(\mathbf A_i \mathbf u_i + \mathbf B_i \mathbf v_i\right) - \frac{\lambda}{\alpha}) \]

• 更新\(u,v\)

\[ \arg\min_{u_i} \|\Omega\mathbf u_i \|_2^2 +\frac{\alpha}{2}\Bigg\Vert \mathbf w - \mathbf g + \sum_{i} \left(\mathbf A_i \mathbf u_i + \mathbf B_i \mathbf v_i\right) + \frac{\lambda}{\alpha}\Bigg\Vert_2^2 \]

\[ \arg\min_{v_i} \|\Omega\mathbf v_i \|_2^2+\frac{\alpha}{2}\Bigg\Vert \mathbf w - \mathbf g + \sum_{i} \left(\mathbf A_i \mathbf u_i + \mathbf B_i \mathbf v_i\right) + \frac{\lambda}{\alpha}\Bigg\Vert_2^2 \]

这两个子问题可通过梯度为零，求最小二乘解 \[ u^{k+1} = (\frac{2}{\alpha} \Omega^T\Omega + \mathbf A_i^T\mathbf A_i)^{-1} \mathbf A_i^T (\mathbf g - \sum_{m \ne i} \mathbf A_m \mathbf u_m - \sum_m \mathbf B_m \mathbf v_m - \mathbf w - \frac{\lambda}{\alpha}) \]

\[ v^{k+1} = (\frac{2}{\alpha} \Omega^T\Omega + \mathbf B_i^T\mathbf B_i)^{-1} \mathbf B_i^T (\mathbf g - \sum_{m} \mathbf A_m \mathbf u_m - \sum_{m \ne i} \mathbf B_m \mathbf v_m - \mathbf w - \frac{\lambda}{\alpha}) \]

简化以上表达式

\[ \mathbf H_{c_i} = (\frac{2}{\alpha} \Omega^T\Omega + \mathbf A_i^T\mathbf A_i)^{-1}, \mathbf r_{c_i} = \mathbf g - \sum_{m \ne i} \mathbf A_m \mathbf u_m - \sum_m \mathbf B_m \mathbf v_m - \mathbf w - \frac{\lambda}{\alpha} \]

\[ \mathbf H_{s_i} = (\frac{2}{\alpha} \Omega^T\Omega + \mathbf B_i^T\mathbf B_i)^{-1}, \mathbf r_{s_i} = \mathbf g - \sum_{m} \mathbf A_m \mathbf u_m - \sum_{m \ne i} \mathbf B_m \mathbf v_m - \mathbf w - \frac{\lambda}{\alpha} \]

\(\mathbf H_{c_i}, \mathbf H_{s_i}\)是低通滤波器，\(\mathbf r_{c_i}, \mathbf r_{s_i}\)是剔除其他信号和噪声后的残差信号。 \[ \mathbf g_i^{k+1} = \mathbf A_i \mathbf u_i^{k+1} + \mathbf B_i \mathbf v_i^{k+1} = \mathbf A_i \mathbf H_{c_i} \mathbf A_i^T \mathbf r_{c_i} + \mathbf B_i \mathbf H_{s_i} \mathbf B_i^T \mathbf r_{s_i} \]

注记：与Vold-Kalman filter类似，二阶导的\(\ell_2\)范数估计带宽的原理本质上是时频滤波器组，而每个滤波器共享相似的性质。上式的\(\mathbf A_i \mathbf H_{c_i} \mathbf A_i^T\)与\(\mathbf B_i \mathbf H_{s_i} \mathbf B_i^T\)分别对残差信号\(\mathbf r_{c_i}\)、\(\mathbf r_{s_i}\)进行低通滤波。包含在\(\mathbf A_i,\mathbf B _i\)的瞬时频率可以估计中心频率，惩罚参数\(\alpha\)决定得到信号的光滑程度。\(\alpha\)越小，信号越光滑，滤波器允通过的带宽越窄。

• 通过反正切解调技术更新瞬时频率的增量

\[ \begin{aligned} \Delta \tilde{f}_{i}^{k+1}(t) &=-\frac{1}{2 \pi} \frac{d}{d t}\left(\arctan \left(\frac{v_{i}^{k+1}(t)}{u_{i}^{k+1}(t)}\right)\right) \\ &=\frac{v_{i}^{k+1}(t) \cdot\left(u_{i}^{k+1}(t)\right)^{\prime}-u_{i}^{k+1}(t) \cdot\left(v_{i}^{k+1}(t)\right)^{\prime}}{2 \pi\left(\left(u_{i}^{k+1}(t)\right)^{2}+\left(v_{i}^{k+1}(t)\right)^{2}\right)} \end{aligned} \]

假设瞬时频率为光滑函数，其增量在每次迭代的仍是带宽受限函数 \[ \min_{\Delta \mathbf f_i^{k+1}} \|\Omega \Delta \mathbf f_i^{k+1}\|_2^2 +\frac{\mu}{2}\|\Delta \mathbf f_i^{k+1}-\Delta {\hat {\mathbf f}}_i^{k+1}\|_2^2 \] 通过反正切得到\(\Delta {\hat {\mathbf f}}_i^{k+1}\)，解为 \[ \Delta f_i^{k+1} = (\frac{2}{\mu} \Omega^T\Omega +I)^T \Delta {\hat {\mathbf f}}_i^{k+1} \]

• 更新Lagrangian乘子

\[ \lambda ^{k+1} = \lambda ^{k} + \alpha (\mathbf w^{k+1} + \sum_i \mathbf g_i^{k+1} - \mathbf g) \]

VNCMD算法流程

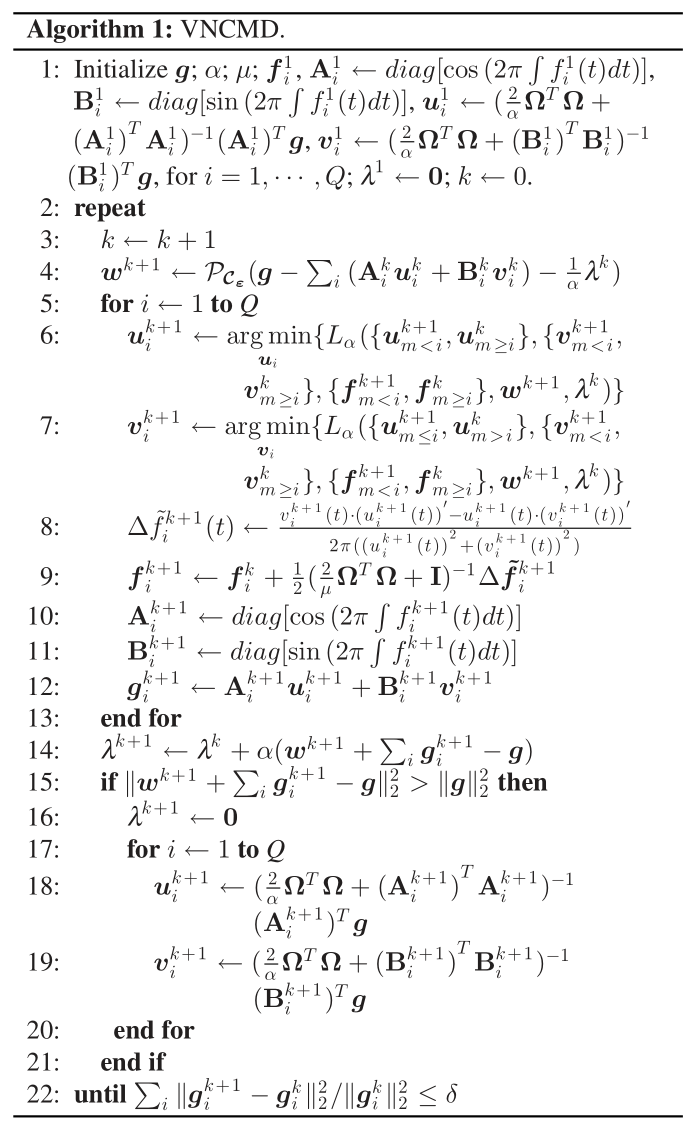
自适应版本

最近同一团队又提出自适应线性调频模态追踪算法(adaptive chirp mode pursuit, ACMP)^[2]，以递归地形式获取模态，该算法可处理如下缺陷：

• 模态数的先验
• 经验地将带宽设为固定值
• 算法依赖初始化

\[ \begin{aligned} &\min_{u_i,v_i,{\hat f}_i} \|u_i^{\prime\prime} (t)\|_2^2 + \|v_i^{\prime\prime} (t)\|_2^2 + \tau \|x(t) - x_i (t)\|_2^T \\ &\text{s.t.} x_i(t) = u_i(t)\cos(2\pi \int_0^t \hat f_i(s) ds) + v_i(t)\sin(2\pi \int_0^t \hat f_i(s) ds)\|_2 \end{aligned} \] 目标函数的第三项表示残差信号的能量，这是一种贪婪算法的形式，通过不断地迭代使得残差趋于零。将等式约束条件带入目标函数并化简，得到如下目标函数 \[ J_\tau (\mathbf y_i, \mathbf f_i) = \|\Phi \mathbf y_i\|_2^2 + \tau \| \mathbf x-\mathbf K_i \mathbf y_i\|_2^2 \] 其中 \[ \begin{aligned} \mathbf x &= [x(t_0), \dots, x(t_{N-1})]^T\\ \mathbf f_i &= [\hat f_i(t_0), \dots, \hat f_i(t_{N-1})]^T\\ \mathbf y_i &= [\mathbf u_i^T \quad \mathbf v_i^T]^T\\ \mathbf u_i &= [u_i(t_0), \dots, u_i(t_{N-1})]^T\\ \mathbf v_i &= [v_i(t_0), \dots, v_i(t_{N-1})]^T\\ \mathbf K_i &= [\mathbf C_i \quad \mathbf S_i]\\ \mathbf C_i &= \operatorname{diag}[\cos \varphi_i(t_0), \dots, \cos \varphi_i(t_{N-1})]\\ \mathbf S_i &= \operatorname{diag}[\sin \varphi_i(t_0), \dots, \sin \varphi_i(t_{N-1})]\\ \varphi_i(t) &=2\pi \int_0^t \hat f_i(s)ds\\ \Phi &= \left[\begin{matrix} \mathbf D & \mathbf 0 \\ \mathbf 0 & \mathbf D\end{matrix}\right] \end{aligned} \] 二阶导数用矩阵算子离散表示 \[ \mathbf D = \left[\begin{matrix} 1 & -2 & 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & -2 & 1 & 0 & \cdots & 0 \\ \vdots & \ddots & \ddots & \ddots & \ddots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 & -2 & 1 & 0 \\ 0 & \cdots & 0 & 0 & 1 & -2 & 0 \end{matrix}\right] \] （最小二乘）令目标函数梯度为令，即\(\frac{\partial J_\tau(\mathbf y_i,\mathbf f_i)}{\partial \mathbf y_i} = 0\)，得 \[ \mathbf y_i^n = [\mathbf u_i^n \quad \mathbf v_i^n]^T = (\frac{1}{\tau}\mathbf\Phi^T \mathbf\Phi +(\mathbf K_i^n)^T \mathbf K_i^n)^{-1} (\mathbf K_i^n)^T \mathbf x \] 目标信号可通过\(\mathbf x_i^n = \mathbf K_i^n \mathbf y_i^n\)获得。因为\(J_\tau(\mathbf y_i,\mathbf f_i)\)关于\(\mathbf f_i\)高度非线性，因此梯度为零得方法不可取。在VNCMD算法里采用反正切解调获取瞬时频率的增量，再结合上式频率函数的光滑性假设，增量\(\Delta\mathbf f_i\)满足低通性 \[ \min_{\Delta \mathbf f_i^{n}} \|\mathbf D \Delta \mathbf f_i^{n}\|_2^2 +\mu\|\Delta \mathbf f_i^{n}-\Delta {\hat {\mathbf f}}_i^{n}\|_2^2 \] 不难求出增量的显示表达式，因此瞬时频率可通过\(\mathbf f_i^{i+1} = \mathbf f_i^n + \Delta \mathbf f_i^n\)更新

ACMP算法流程

追踪思想

考虑信号模型 \[ x = \hat x_m + \hat r_m \] 最优的目标模态应该是原始信号在由线性调频模态所张成的信号空间上的正交投影，因此 \[ \hat x_m^T \hat r_m = 0 \iff \frac{\hat x_m^T \hat x_m}{\hat x_m^T x} = 1 \] 令\(R(\tau, K_m) = K_m (\frac{1}{\tau^2} \Phi^T \Phi + \frac{1}{\tau} K_m^t K_m)^{-1}K_m^T\)，则\(x_m = \frac{1}{\tau} R(\tau, K_m) x\)，利用正交关系可得到最优带宽参数\(\tau\)的更新公式 \[ \tau^{n+1} = \frac{x^T R(\tau^n, K_m^n)^TR(\tau^n, K_m^n)x }{x^T R(\tau^n, K_m^n)^T x} = \frac{\tau^n (x_m^n) ^T }{(x_m^n) ^Tx} \]

ACMP算法流程+自适应带宽

多元版本

补充一个多元变分非线性线性调频模态分解算法(Multivariate nonlinear chirp mode decomposition)^[3]。

多元非线性线性调频模态

类似VMD到MVMD的转变，首先给出多元模态的定义 \[ \mathbf{g}(t)=\left[\begin{array}{c} g_{1}(t) \\ g_{2}(t) \\ \vdots \\ g_{C}(t) \end{array}\right]=\left[\begin{array}{c} a_{1}(t) \cos(2\pi \int_0^t f_1(s)ds + \phi_{1})\\ a_{2}(t) \cos(2\pi \int_0^t f_2(s)ds + \phi_{2})\\ \vdots \\ a_{M}(t) \cos(2\pi \int_0^t f_M(s)ds + \phi_{M}) \end{array}\right] \] 通过Hilbert变换得到的如下解析信号 \[ \begin{aligned} \mathbf g_A (t) &= \mathbf g(t) + j{\mathcal H}(\mathbf g(t)) \\ &=\left[\begin{array}{c} g_{1,A}(t) \\ g_{2,A}(t) \\ \vdots \\ g_{M,A}(t) \end{array}\right]=\left[\begin{array}{c} a_{1}(t) \exp(j(2\pi \int_0^t f_1(s)ds + \phi_{1}))\\ a_{2}(t) \exp(j(2\pi \int_0^t f_2(s)ds + \phi_{2}))\\ \vdots \\ a_{M}(t) \exp(j(2\pi \int_0^t f_M(s)ds + \phi_{M})) \end{array}\right]\\ &=\left[\begin{array}{c} a_{1}(t) \\ a_{2}(t) \\ \vdots \\ a_{M}(t) \end{array}\right] \exp(j(2\pi \int_0^t f(s)ds + \phi)) = \mathbf a(t)\exp(j(2\pi \int_0^t f(s)ds + \phi)) \end{aligned} \]

上式的变换是基于不同成分的模态具有共同的频率成分，这也有利于模态对准(mode-alignment)。

目标函数

• 连续形式

\[ \begin{aligned} &\min_{u_i(t),v_i(t),{\hat f}_i(t)} \sum_{i=1}^Q \sum_{m=1}^M \left(\|u_{i,m}^{\prime\prime} (t)\|_2^2 + \|v_{i,m}^{\prime\prime} (t)\|_2^2 \right) \\ &\text{s.t.} \|x_m(t) - \sum_{i=1}^Q u_{i,m}(t)\cos(2\pi \int_0^t \hat f_i(s) ds) + v_{i,m}(t)\sin(2\pi \int_0^t \hat f_i(s) ds)\|_2 \leq \varepsilon_m \end{aligned} \]

• 离散形式

\[ \begin{aligned} &\min_{\mathbf u_i, \mathbf v_i, \mathbf f_i} \sum_{i} \sum_{m} \left(\|\Omega\mathbf u_{i,m} \|_2^2 + \|\Omega\mathbf v_{i,m} \|_2^2\right)\\ &\text{s.t.} \left\|\mathbf x_m - \sum_{i} \left(\mathbf A_i \mathbf u_{i,m} + \mathbf B_i \mathbf v_{i,m}\right)\right\|_2 \leq \varepsilon_m \end{aligned} \]

使用ADMM算法迭代，与NCMD算法区别的是模态对准导致瞬时频率更新公式需要对所有模态频率进行平均 \[ \mathbf f_i^{k+1}(t_n) = \frac{\sum_m \mathbf f_{i,m}^{k+1}(t_n) |\mathbf a_{i,m}^{k+1}(t_n)|^2}{\sum_m |\mathbf a_{i,m}^{k+1}(t_n)|^2} \] 其中\(\mathbf a_{i,m}^{k+1} = \sqrt{(\mathbf u_{i,m}^{k+1})^2 + (\mathbf v_{i,m}^{k+1})^2}\)

MNCMD算法流程

MNCMD vs MVMD

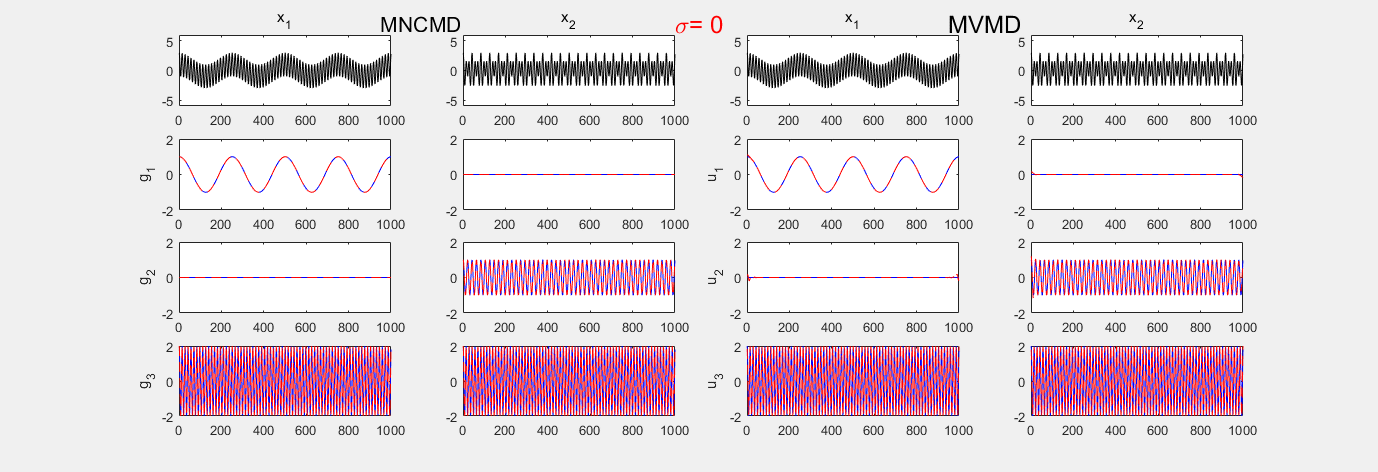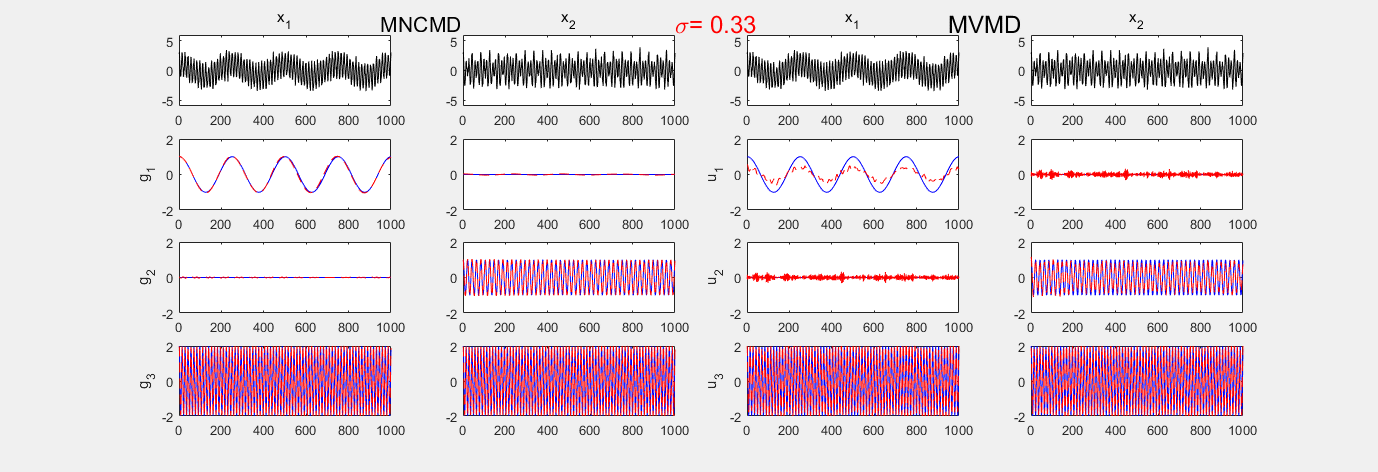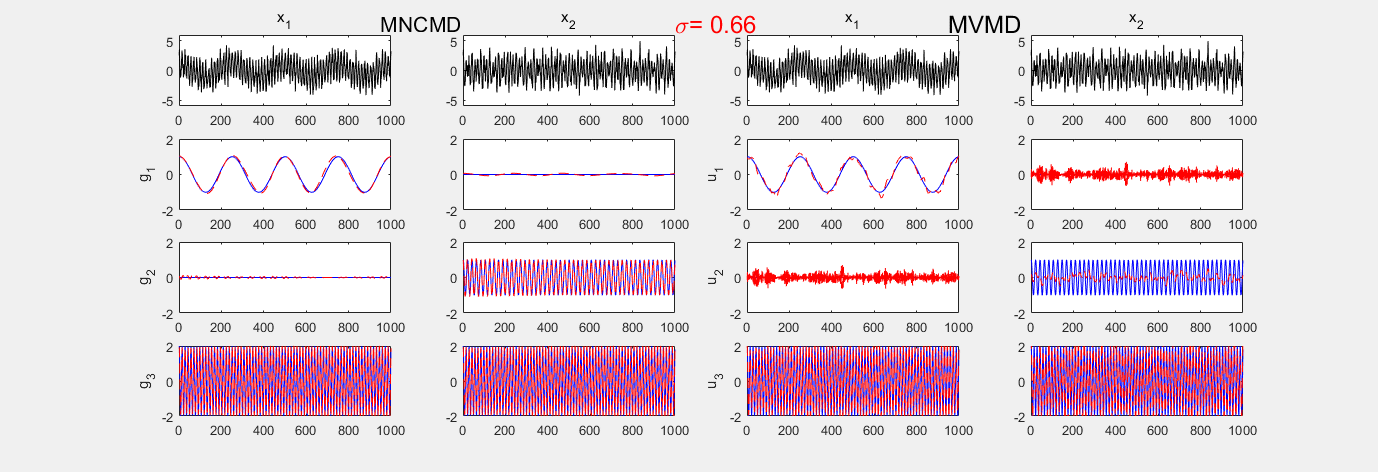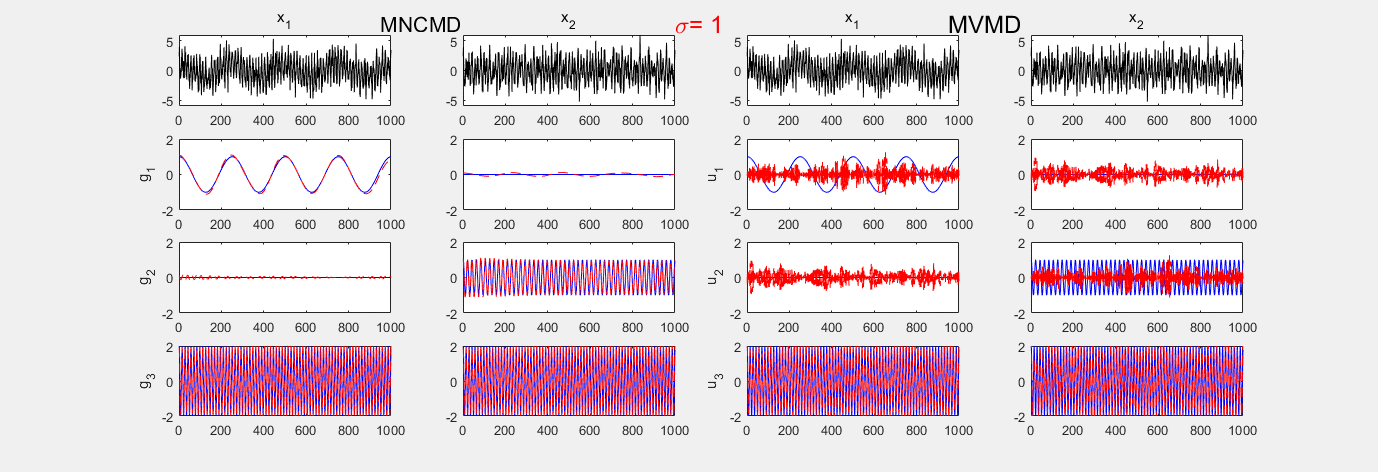
参考文献

1. Chen S , Dong X , Peng Z , et al. Nonlinear Chirp Mode Decomposition: A Variational Method[J]. IEEE Transactions on Signal Processing, 2017, 65(22):6024-6037. ↩︎
2. Chen S, Yang Y, Peng Z, et al. Adaptive chirp mode pursuit: Algorithm and applications[J]. Mechanical Systems and Signal Processing, 2019: 566-584. ↩︎
3. Qiming Chen, Lei Xie, Hongye Su, Multivariate nonlinear chirp mode decomposition[J]. Signal Processing, Volume 176, November 2020, 107667 ↩︎