写在前面

以前看算法时，Majorization-Minimization算法经常出现，借助一些blog^[1]和slide^[2]\(^,\)^[3]\(^,\)^[4]\(^,\)^[5]\(^,\)^[6]来总结下。

MM算法是什么

MM算法是优化领域的一个重要方法。与其说它是一个具体算法，不如说是一个算法框架，因为很多具体的算法都可以被推断成MM算法，例如坐标下降法(coordinate descent)、近端梯度法(proximal gradient)、EM算法等等。

回到MM算法。复杂的优化问题不方便直接处理时，通常期望找到一个近似的问题或者近似的解来间接解决原问题。再看算法名字 \[ \text{Majorization}+\text{Minimization} \] 当然，该算法也存在反面 \[ \text{Minorization}+\text{Maximization} \] 显然意味着两个步骤交替进行

• 找到一个可以控制迭代点趋于最优解的优化函数
• 求解该近似函数为目标的最优化

从数学角度来说，MM算法的核心思想是连续上限最小化(Successive upper bound minimization)，设计一系列近似的优化(majorizing)函数来控制原函数的上限，通过最小化序列来收敛至原目标的最优解。

简单来说，MM算法将原始的优化问题转化为一系列简单的优化问题，让求解变得更简单。

优化函数定义

目标函数\(f(x)\)在点\(x_k\)处的优化函数\(g(x|x_k)\)满足两点性质

• 占优条件(dominance condition) \[ g(x | x_k) \ge f(x), \quad \forall x \]

• 切线条件(tangent condition) \[ g(x_k | x_k) = f(x_k), \quad \forall x_k \]

即\(g(x|x_k)\)在\(f(x)\)上方且相切于点\(x= x_k\)。

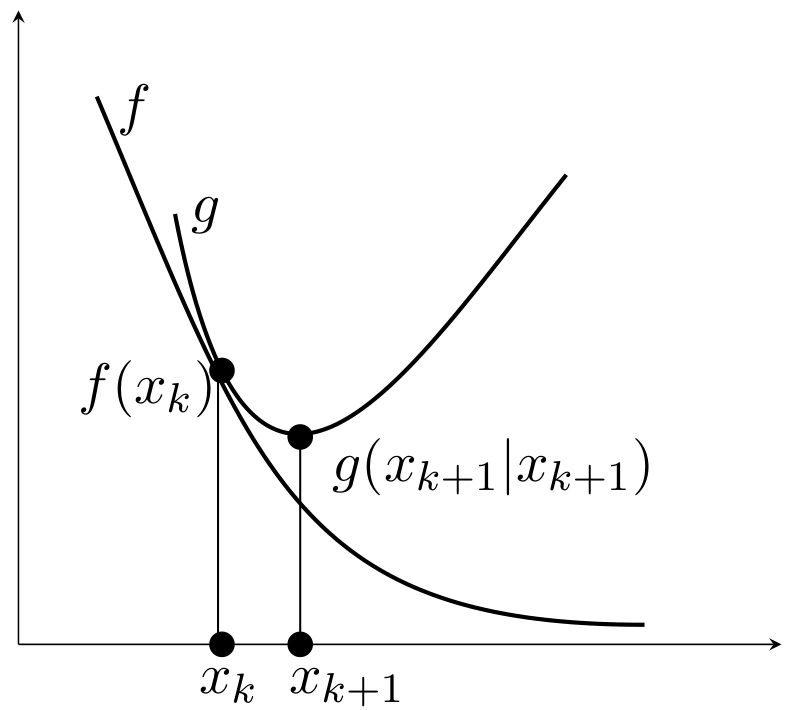
只要满足这两个条件，如下迭代产生的序列必能收敛至局部最优解。 \[ x_{k+1} = \arg\min_x g(x|x_k) \] 这是因为 \[ f(x_{k+1}) \leq g(x_{k+1}|x_k) \leq g(x_k|x_k) = f(x_k) \] 注意：

• MM算法得到的序列保证目标函数值非增
• 更新的序列点用于构造下一代的优化函数
• 优化函数通常用于分裂参数(split parameters)，从而可以逐元素进行更新。

MM过程可视化

• 蓝色：原始的目标函数
• 绿色：一系列优化函数
• 红色：切点的选择

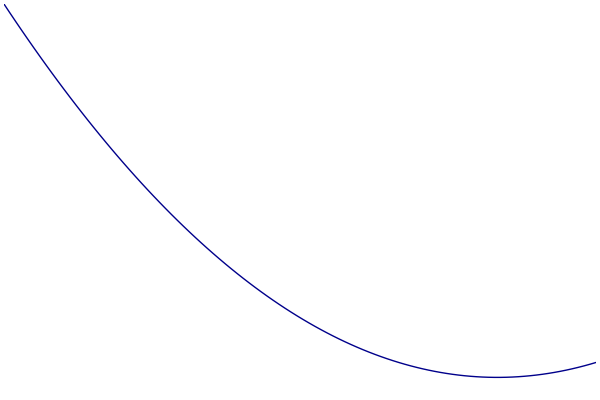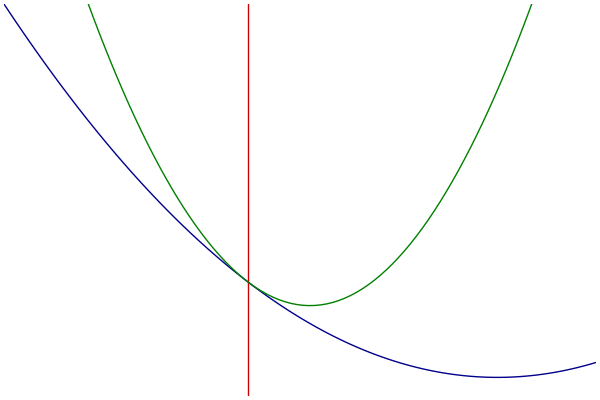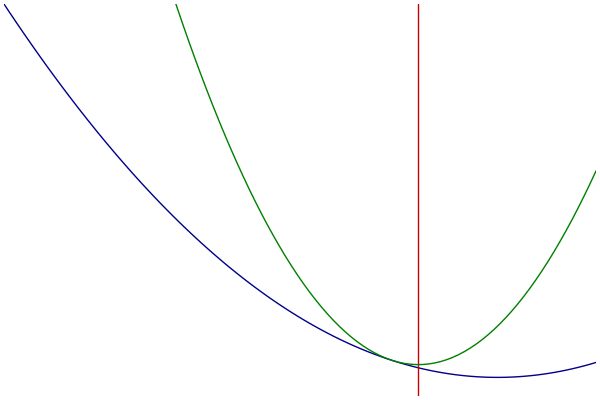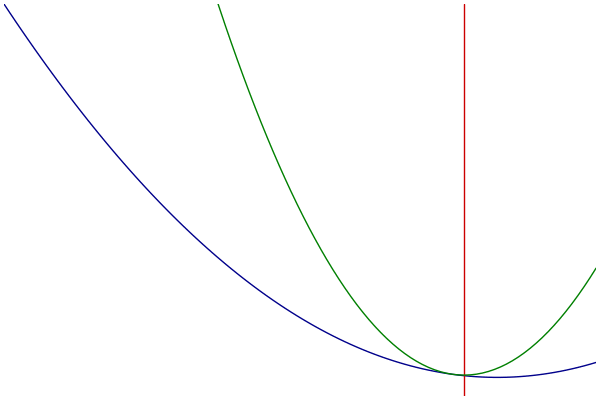
优化函数的构造

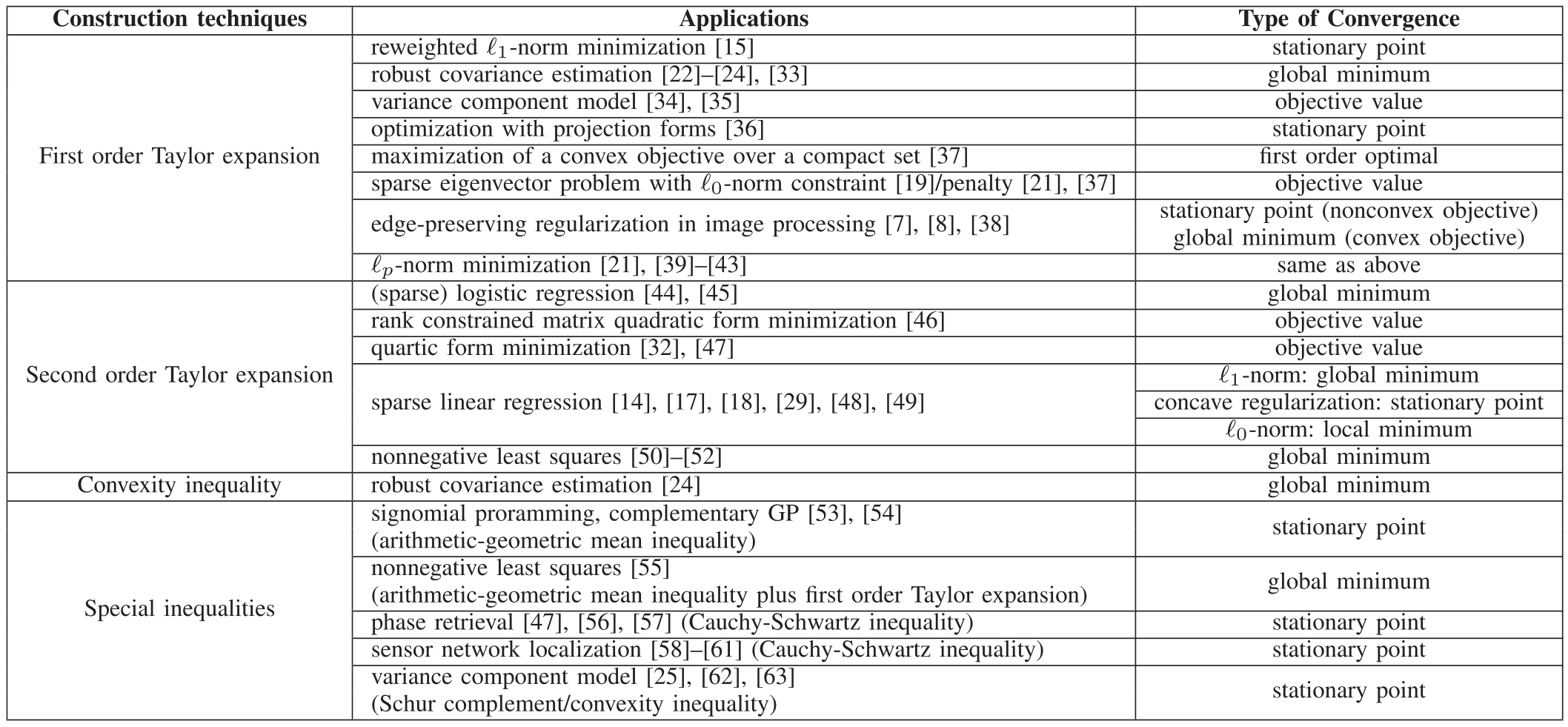
选择合适的优化函数尤为重要，通常有四种方式^[7]：一阶泰勒展开、二阶泰勒展开、凸性不等式和特殊不等式。

一阶泰勒展开

一阶可微函数\(f\)在点\(x_0\)处的泰勒展开为 \[ f(x)=f\left(x_{0}\right)+\nabla f^{T}\left(x_{0}\right)\left(x-x_{0}\right)+\mathcal O \]

• 若\(f\)为凹函数，一阶泰勒展开是\(f\)的全局向下估计(underestimator)，对应于Minorization Maximization，即 \[ f(x) \geq f\left(x_{0}\right)+\nabla f^{T}\left(x_{0}\right)\left(x-x_{0}\right) \]

• 若\(f\)为凸函数，一阶泰勒展开是\(f\)的全局向上估计(overestimator)，对应于Majorization Minimization，即 \[ f(x) \leq f\left(x_{0}\right)+\nabla f^{T}\left(x_{0}\right)\left(x-x_{0}\right) \]

二阶泰勒展开

若函数\(f\)是二阶可微的，在点\(x_k\)处的泰勒展开为 \[ \begin{aligned} f(x)=&f\left(x_{k}\right)+\nabla f^{T}\left(x_{k}\right)\left(x-x_{k}\right)\\ &+\frac{1}{2}\left(x-x_{k}\right)^{T} \nabla^{2} f(\xi)\left(x-x_{k}\right)+\mathcal O \end{aligned} \] 对应的优化函数可设置为二次函数 \[ \begin{aligned} g(x|x_k) =& f\left(x_{k}\right)+\nabla f^{T}\left(x_{k}\right)\left(x-x_{k}\right) \\ &+\frac{1}{2}\left(x-x_{k}\right)^{T} M \left(x-x_{k}\right) \end{aligned} \] 其中\(M \succeq \nabla^{2} f(x),\forall x\)，即\(M - \nabla^{2} f(x)\)为半正定矩阵，则有 \[ g(x|x_k) - f\left(x\right) = \frac{1}{2}\left(x-x_{k}\right)^{T} \left(M - \nabla^{2} f(\xi)\right) \left(x-x_{k}\right) \geq 0 \] 说明\(g\)控制了\(f\)。\(M\)的选择不唯一，通常选\(M = \nabla^{2} f(x) + \delta I\)。

选择二阶泰勒展开作为优化函数\(g(x|x_k)\)后，迭代更新存在闭形式 \[ x_{k+1} = x_k - M^{-1}\nabla f(x_k). \] 可以理解为二次函数求极小点，而更新公式类似于Newton法，但使用了保证目标函数下降的Hessian矩阵的近似。

应用

最小二乘

考虑一个最小二乘问题 \[ f(x) = \|Ax-b\|_2^2 \] 其一阶导和二阶导计算如下： \[ \begin{aligned} \nabla f(x) &= 2A^T(Ax-b) \\ \nabla^{2} f(x) &= 2A^TA \end{aligned} \] 因此\(f\)在点\(x_k\)处的二阶泰勒展开式为 \[ \begin{aligned} f(x) = &f(x_k) + 2A^T(Ax_k-b)(x-x_k)\\ & + 2(x-x_k)^TA^TA(x-x_k) \end{aligned} \] 构造优化函数 \[ \begin{aligned} g(x|x_k) = &f(x_k) + 2A^T(Ax_k-b)(x-x_k)\\ & + 2(x-x_k)^TM(x-x_k) \end{aligned} \] 其中仅需要对角阵满足\(M\succeq A^TA\)，可以取\(M = A^TA + \delta I\)，其中\(\delta > 0\)。

非负矩阵分解

给定向量\(x\)，非负矩阵分解模型如下 \[ f(W,h) = \|Wh-x\|_2^2 \] 同样做二阶泰勒展开 \[ \begin{aligned} f(W,h) =& f(h_k) + 2W^T(Wh_k-x)(h-h_k) \\ &+ 2(h-h_k)^TW^TW(h-h_k) \end{aligned} \] 取对角矩阵\(M = \text{diag}(\frac{[W^TWh]_i}{[h]_i})\)，则有\(M\succeq W^TW\)，对应的优化函数为 \[ \begin{aligned} g(W,h|h_k) =& f(h_k) + 2W^T(Wh_k-x)(h-h_k) \\ &+ 2(h-h_k)^TM(h-h_k) \end{aligned} \]

Logistic回归

利用样本\(x_i\)以及二元响应变量\(y_i\in\{0, 1\}\)，训练回归模型如下： \[ f(\beta) = \sum_i \left\{-y_i x_i^T\beta + \ln\left[1 + \exp(x_i^T\beta)\right]\right\} \] 其一阶导和二阶导计算如下： \[ \begin{aligned} \nabla f(\beta) &= \sum_i -[y_i - \hat{y_i}(\beta)]x_i \\ \nabla^{2} f(\beta) &= \sum_i \hat{y_i}(\beta)[1 - \hat{y_i}(\beta)]x_i x_i^T \end{aligned} \] 设\(\hat{y}_i(\beta) = (1 + \exp(-x_i^T\beta))^{-1}\)，下面构造优化函数：

• Hessian矩阵形式为\(\nabla^{2} f(\beta) = X^TWX\)，其中对角矩阵\(W\)的对角元素为\(\hat{y}_i(1 - \hat{y}_i)\)
• \(\hat{y}_i\in (0,1)\)，所以\(\frac{1}{4} \ge \hat{y}_i(1 - \hat{y}_i)\)
• 选择\(M = X^TX/4\)则可构造二次上限(quadratic upper bound)

更新规则如下

• MM算法 \[ \beta^{(t+1)} = \beta^{(t)} - 4\left(X^TX\right)^{-1}X^T(y - \hat{y}(\beta^{(t)})) \] 整个过程只需要计算一次矩阵的逆\((X^TX)^{-1}\)

• Newton算法 \[ \beta^{(t+1)} = \beta^{(t)} - \left(X^TWX\right)^{-1}X^T(y - \hat{y}(\beta^{(t)})) \] 每次迭代需反复计算矩阵的逆\(\left(X^TWX\right)^{-1}\)

这个例子不难发现，目标函数\(f\)是光滑的凸函数，所以只需要找到函数二阶导的上界，就能利用二阶泰勒展开式，很容易构造出一系列优化函数，此外优化函数的最小化存在闭解，为原问题减少了大量的计算成本。

DC programming

假设函数\(f\)可表示两个可微的凸函数之差，即 \[ f(x) = g(x) - h(x) \] 通常认为\(f\)是非凸的，因此传统的凸分析算法不再适用，但是该函数可分解为凸函数(\(g\))与凹函数(\(-h\))之和，因此不妨对后者进行一阶展开得到线性函数(既是凸函数又是凹函数) \[ u(x|x_k) = g(x) - \left(h(x_k)+\nabla h^{T}\left(x_{k}\right)\left(x-x_{k}\right)\right) \] 不难看出

• \[ u(x|x_k) \geq f(x), \quad \forall x \]

• \[ u(x_k|x_k) = f(x_k) \]

则线性化后的表示\(u(x|x_k)\)可作为优化函数来控制原函数\(f(x)\)。

\(\ell_2 - \ell_p\)优化问题

考虑如下常见的优化问题(\(p\geq 1\)) \[ f(x) = \frac{1}{2} \|Ax-y\|_2^2 + \mu\|x\|_p \]

• 当矩阵\(A\)为单位阵或酉阵时，最优解存在闭解形式 \[ x^* = A^Ty - \text{Proj}_C(A^Ty) \]

  • \(C=\{x:\|x\|_{p^*} \leq \mu\}\)
  • \(\|\cdot\|_{p^*}\)是\(\|\cdot\|_{p}\)的对偶范数
  • \(\text{Proj}_C\)是投影算子
  • 当\(p=1\)时，最优解可用软阈值算子(soft-thresholding)表示

• 对于更一般形式的矩阵\(A\)，不存在闭解形式的最优解，下面就用MM算法来给出迭代步骤。

关键在于构造优化函数，首先定义如下距离函数 \[ \text{dist}(x|x_k) = \frac{c}{2}\|x-x_k\|_2^2 - \frac{1}{2}\|Ax-Ax_k\|_2^2 \] 其中参数\(c\)满足\(c>\lambda_{\max}(A^TA)\)。显然有

• \[ \text{dist}(x|x_k) \geq 0,\forall x \]

• \[ \text{dist}(x_k|x_k) = 0 \]

将\(\text{dist}(x|x_k)\)加到原函数上则可作为优化函数来控制原函数\(f(x)\)。 \[ \begin{aligned} g(x|x_k) &= f(x) + \text{dist}(x|x_k)\\ &= \frac{c}{2}\|x-\bar x_k\|_2^2 + \mu \|x\|_p + \text{const} \end{aligned} \] 其中 \[ \bar x_k = \frac{1}{c}A^T(y-Ax_k) + x_k \] 另外，原函数\(f\)不存在显式的最优解，而优化函数\(g(x|x_k)\)存在显式的最优解(退化到矩阵\(A\)为单位阵这一特殊情形)。

期望最大化（EM）算法

给定一个随机观察变量\(w\)，用对数似然函数最小化来估计\(\theta\) \[ \hat \theta _{\text{ML}} = \arg\min_\theta -\ln p(w|\theta) \]

• E-step \[ g(\theta,\theta^r) = \mathbb E_{z|w,\theta^r}\{\ln p(w,z|\theta)\} \]

• M-step \[ \theta^{r+1} = \arg\min_\theta g(\theta,\theta^r) \]

迭代产生一个\(\{-\ln p(w|\theta^r)\}\)的非减序列。

对目标函数运用Jensen不等式可得到优化函数 \[ \begin{aligned} &\begin{aligned} &-\ln p(w \mid \theta) \\ =&-\ln \mathbb{E}_{z \mid \theta} p(w \mid z, \theta) \\ =&-\ln \mathbb{E}_{z \mid \theta}\left[\frac{p\left(z \mid w, \theta^{r}\right) p(w \mid z, \theta)}{p\left(z \mid w, \theta^{r}\right)}\right] \end{aligned}\\ &=-\ln \mathbb{E}_{z \mid w, \theta^{r}}\left[\frac{p(z \mid \theta) p(w \mid z, \theta)}{p\left(z \mid w, \theta^{r}\right)}\right] (\text{interchange integrations})\\ &\leq-\mathbb{E}_{z \mid w, \theta^{r}} \ln \left[\frac{p(z \mid \theta) p(w \mid z, \theta)}{p\left(z \mid w, \theta^{r}\right)}\right] (\text{Jensen's inequality})\\ &\begin{array}{l} =-\mathbb{E}_{z \mid w, \theta^{r}} \ln p(w, z \mid \theta)+\mathbb{E}_{z \mid w, \theta^{r}} \ln p\left(z \mid w, \theta^{r}\right) \\ \triangleq u\left(\theta, \theta^{r}\right) \end{array} \end{aligned} \]

• \(u\left(\theta, \theta^{r}\right)\)是\(-\ln p(w|\theta)\)的优化函数

  • \[ u\left(\theta, \theta^{r}\right) \geq -\ln p(w|\theta), \forall \theta \]

  • \[ u\left(\theta^{r}, \theta^{r}\right) = -\ln p(w|\theta^{r}) \]

• EM算法与MM算法的联系

  • \(u(\theta, \theta^{r})\)与\(\theta\)有关的只有第一项
  • E-step本质上是构建\(u(\theta, \theta^{r})\)，等价于构建\(g(\theta, \theta^{r})\)
  • M-step最小化\(u(\theta, \theta^{r})\)，等价于最小化\(g(\theta, \theta^{r})\)

优势 or 原理

体现在

• 避免矩阵求逆
• 分离问题的参数（并行计算）
• 使优化问题线性化（DC programming）
• 优雅地处理平等和不平等的约束
• 恢复对称性
• 将一个非平滑问题变成一个平滑问题
• 优化函数优化的闭解

迭代计算则是需要付出的代价。

参考文献

1. https://seqstat.com/blog/2016-12-24-mm-algorithms/ ↩︎
2. Majorization-Minimization Algorithm ↩︎
3. Majorization Minimization - the Technique of Surrogate ↩︎
4. Majorization Minimization (MM) and Block Coordinate Descent (BCD) ↩︎
5. Examples of MM Algorithms ↩︎
6. Generalized Majorization-Minimization ↩︎
7. Y. Sun, P. Babu and D. P. Palomar. Majorization-Minimization Algorithms in Signal Processing, Communications, and Machine Learning, IEEE Transactions on Signal Processing, vol. 65, no. 3, pp. 794-816, 1 Feb.1, 2017. ↩︎