写在前面

介绍核方法中的非线性投影技巧(Nonlinear Projection Trick in Kernel Methods)。

核方法

核方法是将数据通过核函数转化为核矩阵，再运用模式识别算法进行分析。因此，核方法提供了模块化框架

• 在高维（甚至无限维）向量空间中映射数据。
• 在这样的空间中寻找（线性）关系。

如果映射选得足够合适，再复杂的关系也可以简化且容易检测到。

p.s. 这也意味着需要大量尝试核函数并探索先验信息。多核学习(Multiple Kernel Learning)，即基本核函数进行线性组合，通过参数学习来达到更优的结果。当然，这也可能会带来计算复杂和过拟合。

核技巧

核矩阵通过内积或\(\ell_2\)范数的形式描述嵌入空间数据的几何信息，被应用至大量机器学习算法中。但当算法不具备内积或\(\ell_2\)范数的形式时，例如基于\(\ell_1\)范数或非凸度量等优化问题，核技巧将不在适用。

因此，能否通过核方法找到输入数据到嵌入特征空间的直接映射吗？

核空间的几何结构

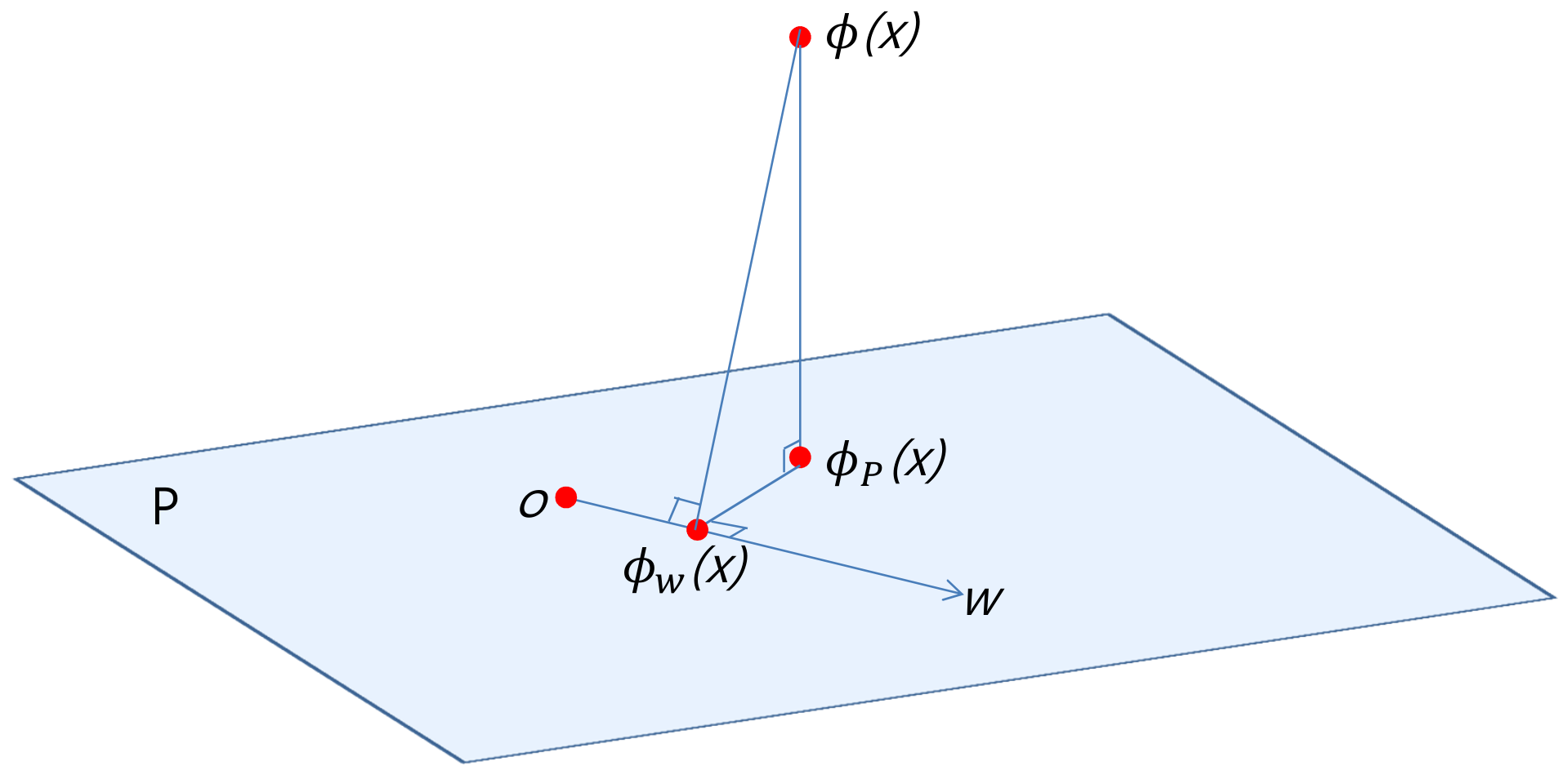
• 训练样本集\(X\)的核映射\(\Phi(X) = [\phi(x_1),\ldots,\phi(x_n)]\)组成特征空间的\(r\)维子空间\(P\)的正交基

设核矩阵\(K = \Phi(X)^T \Phi(X)\)的秩为\(r\)，其特征分解\(K = U \Lambda U^T\)，则矩阵 \[ \Pi = \Phi(X) U \Lambda^{-\frac{1}{2}} \] 的列\(\pi_i = \Phi(X) u_i \lambda_i^{-\frac{1}{2}}\)构成\(P\)的正交基。

• 训练样本\(x\)的核映射\(\phi(x)\)在子空间\(K\)上的投影\(\phi_P(x)\)的坐标

设核向量\(k(x) = \Phi(X)^T\phi(x)\) \[ \phi_P(x) = \Pi\Pi^T\phi(x) = \Pi \Lambda^{-\frac{1}{2}}U^T k(x) \] \(\phi_P(x)\)可视为样本\(x\)到由\(\Pi\)张成子空间的非线性映射，映射后的直接产物为\(x \to y = \Lambda^{-\frac{1}{2}}U^T k(x)\)。

• 样本集\(X\)非线性映射后得到的坐标为

\[ Y = \Lambda^{-\frac{1}{2}}U^T K = \Lambda^{\frac{1}{2}}U^T \]

那么问题来了，坐标唯一吗？注意到： \[ \begin{aligned} K &= U\Lambda U^T = Y^T Y \quad\text{(SVD)}\\ K &= Y^{\prime T}Y^{\prime} \quad\text{(Cholesky decomp)}\\ \Rightarrow Y^{\prime} &= V\Lambda^{\frac{1}{2}}U^T = VY \quad\text{(SVD)} \end{aligned} \] 其中\(Y^{\prime}\)是唯一确定的，而\(V\)是酉阵，因此\(Y\)的结果虽然不唯一，但是仅于\(Y^{\prime}\)存在一个旋转。

• 训练集合的均值

若训练集合核映射后的特征矩阵是以原点为中心的，即满足\(\sum_i \phi(x_i) = 0\)，则映射后的点\(y_i\)也是以原点为中心的，即\(\sum_i y_i = 0\)。但在实际应用中，这一假设过于理想，因此中心化处理非常有必要。

• 残差的坐标

设增广数据集\(X^\prime = [X,x]\)，投影\(\Phi(X^\prime) = [\Phi(X), \phi(x)]\)，残差为\(\delta\phi_P(x) = \phi(x)-\phi_P(x)(\neq 0)\)，则

\(\Phi(X^\prime)\)位于包含\(P\)的\(r+1\)维子空间，\(\Phi(X)\)的坐标为\([Y^T,0]^T\)，\(\phi(x)\)的坐标为\([y^T,\sqrt{k(x,x)-y^Ty}]^T\)。

• \(w\)的坐标

如果空间\(P\)中的向量具有形式\(w=\Phi(X)\alpha\)，则也可表示为\(w = \Pi \beta\)，其中\(\beta = Y \alpha\)为\(w\)在\(P\)中的坐标。

• \(\phi_w(x)\)的坐标

核映射\(\phi(x)\)在\(w\)上的投影\(\phi_w(x) = \Pi \gamma\)，其中\(\gamma = \frac{\beta\beta^T}{\beta^T\beta}y\)为\(\phi_w(x)\)的坐标。

• 中心化

记\(\Psi(X) = [\psi(x_1),\ldots,\psi(x_n)]\)为未中心化数据的特征，其均值\(\bar \psi = \frac{1}{n} \sum_{i=1}^n \psi(x_i)\)。\(\kappa(a,b) = \psi(a)^T\psi(b)\)为未中心化的核函数，\(\mathcal K = \Psi(X)^T\Psi(X)\)为未中心化的核矩阵，\(\kappa(x) = [\kappa(x_1,x),\ldots,\kappa(x_n,x)]^T\)为未中心化的核向量。

中心化特征、中心化核矩阵、中心化核向量 \[ \begin{aligned} \Phi(X) &= \Psi(X) - \bar \psi 1_n^T = \Psi(X)(I_n - E_n)\\ K &= \Phi(X)^T \Phi(X) = (I_n - E_n)\mathcal K(I_n - E_n)\\ k(x) &= \Phi(X)^T \phi(x) = (I_n - E_n)[\kappa(x) - \frac{1}{n}\mathcal K 1_n] \end{aligned} \] 其中，\(E_n = \frac{1}{n} 1_n 1_n^T\)。

核方法

算法应用

KPCA

\[ \arg\min_w \|w^T\Phi(X)\|_2^2 \quad \text{s.t.} \quad \|w\|_2 = 2 \]

• 核技巧

  • 计算散度矩阵\(S_f = \Phi(X)\Phi(X)^T\)的特征分解 \[ S_f w_i = \lambda_i w_i \]

  • 利用\(w = \Phi(X) \alpha\)，得到 \[ K\alpha_i = \lambda_i \alpha_i \]

  • 解 \[ \alpha_i = u_i \lambda_i^{-\frac{1}{2}} \]

  • 非线性特征为 \[ z = W^T\phi(x)=\Lambda_m^{-\frac{1}{2}} U_m^T k(x) \]

• 非线性投影技巧

  • 非线性投影 \[ Y = \Lambda^{\frac{1}{2}}U^T \]

  • 计算散度矩阵 \[ S_Y = YY^T = \Lambda \]

  • 非线性特征 \[ z = \Lambda_m^{-\frac{1}{2}} U_m^T k(x) \]

SVM

\[ \arg\min_{w,b} \frac{1}{2} \|w\|_2^2 \quad \text{s.t.} \quad c_i (w^T\phi(x_i)+b)\geq 1 \quad \forall i \]

• 核技巧

  • Lagrange乘子对偶形式 \[ \begin{aligned} &\arg\max_\alpha \sum_{i=1}^n \alpha_i -\frac{1}{2}\sum_{i,j=1}^n \alpha_i \alpha_j c_i c_j k(x_i,x_j) \\ &\text{s.t.} \quad \sum_{i=1}^n \alpha_ic_i = 0, \alpha_i \geq 0 \quad \forall i \end{aligned} \]

  • \(w\)的结果为 \[ w=\sum_{i=1}^n \alpha_i c_i \phi(x_i) \Rightarrow w^T\phi(x)=\sum_{i=1}^n \alpha_i c_i k(x_i, x) \]

  • \(b\)的结果可由约束条件的KKT条件得到

  • 测试样本\(x\)分类 \[ \text{sgn}(w^T\phi(x)+b) \]

• 非线性投影技巧

  • 非线性投影 \[ Y = \Lambda^{\frac{1}{2}}U^T \]

  • 原始问题 \[ \arg\min_{v,d} \frac{1}{2} \|v\|_2^2 \quad \text{s.t.} \quad c_i (v^T\phi(y_i)+d)\geq 1 \quad \forall i \]

  • 对偶问题 \[ \begin{aligned} &\arg\max_\beta \sum_{i=1}^n \beta_i -\frac{1}{2}\sum_{i,j=1}^n \beta_i \beta_j c_i c_j y_i^T y_j \\ &\text{s.t.} \quad \sum_{i=1}^n \beta_ic_i = 0, \beta_i \geq 0 \quad \forall i \end{aligned} \] 注意：\(k(x_i,x_j) = y_i^Ty_j\)

  • \(v\)的结果为 \[ v=\sum_{i=1}^n \beta_i c_i y_i \]

  • 测试样本\(x\)首先映射为\(y=\Lambda^{-\frac{1}{2}} U^T k(x)\)，再分类 \[ \text{sgn}(v^T\phi(y)+d) \]

PCA-L1

• 原始形式 \[ \arg\max_w\|w^T X\|_1 \quad \text{s.t.} \quad \|w\|_2 =1 \]

• 核技巧 \[ \arg\max_w\|w^T \Phi(X)\|_1 \quad \text{s.t.} \quad \|w\|_2 =1 \] 该问题不是基于\(\ell_2\)范数的优化问题，因此不容易求解。

• 非线性投影技巧

  通过非线性投影\(Y = \Lambda^{\frac{1}{2}}U^T\)后， \[ w=\Pi \beta,\|w\|_2 = \|\beta\|_2 =1, w^T\Phi(X) = \beta^T Y \] 原问题转化为 \[ \arg\max_\beta\|\beta^T Y\|_1 \quad \text{s.t.} \quad \|\beta\|_2 =1 \] 显然，这两问题形式上一致，因此可使用PCA-L1算法（见基于L1范数的主成分分析）来解决KPCA-L1问题。

References

1. Kwak N . Nonlinear Projection Trick in Kernel Methods: An Alternative to the Kernel Trick[J]. IEEE Transactions on Neural Networks & Learning Systems, 2013, 24(12):2113-2119. ↩︎